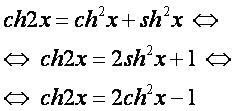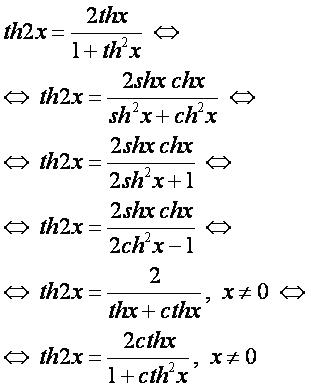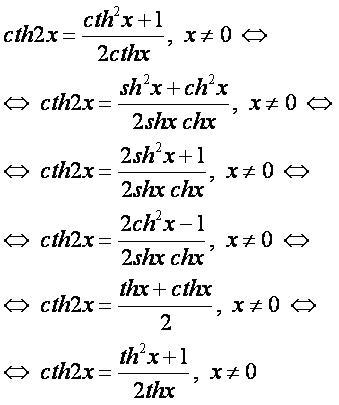Гиперболические функции двойного аргумента — различия между версиями
(начало) |
м |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 14: | Строка 14: | ||
[[файл:ГФКА04.JPG]] | [[файл:ГФКА04.JPG]] | ||
| − | == | + | == [[Функции|Другие формулы]] == |
| − | |||
| − | |||
| − | |||
{{Список ГФА}} | {{Список ГФА}} | ||
| − | |||
== Литература == | == Литература == | ||
* Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.195. | * Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.195. | ||
== Ссылки == | == Ссылки == | ||
* [[Участник:Logic-samara]] | * [[Участник:Logic-samara]] | ||
| − | [[Категория:Математика]][[Категория: | + | [[Категория:Математика]][[Категория:Функции]] |
Текущая версия на 10:28, 21 октября 2024
Гиперболические функции двойного аргумента — это гиперболические функции, в которых двойной аргумент.
Содержание
Формулы
sh(2α)
ch(2α)
th(2α)
cth(2α)
Другие формулы
- гиперболические функции;
- сумма гиперболических функций;
- разность гиперболических функций;
- произведение гиперболических функций;
- гиперболические функции суммы;
- гиперболические функции разности;
- гиперболические функции кратных аргументов;
- гиперболические функции двойного аргумента;
- гиперболические функции половинного аргумента;
- выражение гиперболических функций через другую;
- выражение гиперболических функций через тригонометрические;
- гиперболические функции комплексной переменной;
- производные гиперболических функций;
- дифференциалы гиперболических функций;
- интегралы гиперболических функций;
- графики гиперболических функций.
Литература
- Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.195.