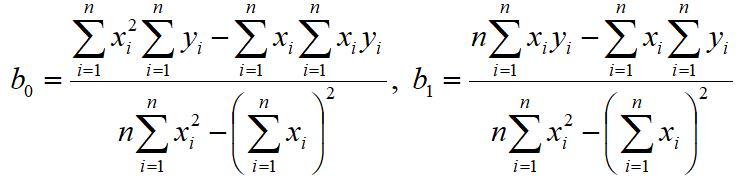Коэффициент линейной регрессии — различия между версиями
м |
м |
||
| Строка 8: | Строка 8: | ||
'''y=b<sub>0</sub>+b<sub>1</sub>x''' — линейное уравнение регрессии; | '''y=b<sub>0</sub>+b<sub>1</sub>x''' — линейное уравнение регрессии; | ||
| − | [[файл:MXn2.png]] — матрица значений независимой переменной в выборке; | + | [[файл:MXn2.png]] — матрица значений независимой переменной в выборке; |
| + | [[файл:Vyn.png]] — значения зависимой переменной. | ||
== Формула == | == Формула == | ||
[[файл:КУЛР01.png]] | [[файл:КУЛР01.png]] | ||
| Строка 15: | Строка 16: | ||
== [[Коэффициенты|Другие коэффициенты]] == | == [[Коэффициенты|Другие коэффициенты]] == | ||
{{Список КФ}} | {{Список КФ}} | ||
| − | |||
== Ссылки == | == Ссылки == | ||
*Википедия. Регрессионный анализ. | *Википедия. Регрессионный анализ. | ||
[[Категория:Математика]][[Категория:Статистика]][[Категория:Математическая статистика]] | [[Категория:Математика]][[Категория:Статистика]][[Категория:Математическая статистика]] | ||
Версия 11:00, 25 октября 2024
Коэффициент линейной регрессии — коэффициент линейного уравнения регрессии с одной независимой переменной.
Содержание
Обозначения
n — число значений в выборке;
b0, b1 — коэффициенты уравнения линейной регрессии;
y=b0+b1x — линейное уравнение регрессии;
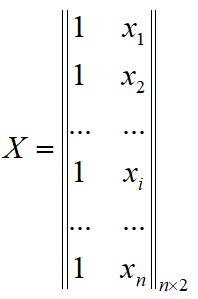— матрица значений независимой переменной в выборке;
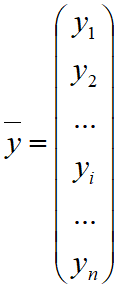— значения зависимой переменной.
Формула
- Для проверки значимости коэффициента линейной регрессии используется гипотеза о коэффициенте линейного уравнения регрессии равном нулю.
Другие коэффициенты
- коэффициент вариации;
- линейный коэффициент вариации;
- коэффициент ковариации;
- коэффициент осцилляции;
- коэффициент парной корреляции;
- коэффициент линейной регрессии;
- коэффициент множественной корреляции;
- коэффициент множественной регрессии;
- коэффициент ранговой корреляции Спирмена;
- коэффициент ранговой корреляции Кендалла;
- коэффициент корреляции Фехнера;
- коэффициент детерминации;
- коэффициент конкордации Кендалла;
- коэффициент ассоциации;
- коэффициент контингенции;
- коэффициент взаимной сопряжённости;
- коэффициент взаимной сопряжённости Пирсона;
- коэффициент взаимной сопряжённости Чупрова;
- коэффициент дифференциации;
- коэффициент Гатева;
- коэффициент Салаи;
- коэффициент Рябцева.
Ссылки
- Википедия. Регрессионный анализ.
