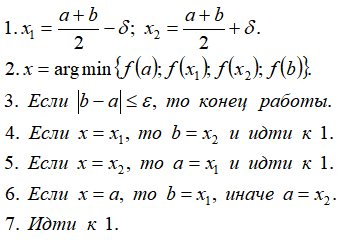Метод дихотомии для оптимизации — различия между версиями
(начало) |
м |
||
| Строка 18: | Строка 18: | ||
*Заметим, что для нахождения решения '''x''', максимизирующего выпуклую функцию '''f(x)''' на отрезке, алгоритм решения модифицируется в части строки 2, она меняется на строку вида: | *Заметим, что для нахождения решения '''x''', максимизирующего выпуклую функцию '''f(x)''' на отрезке, алгоритм решения модифицируется в части строки 2, она меняется на строку вида: | ||
| − | [[файл: | + | [[файл:МДИ02.png]] |
== [[Методы нахождения экстремумов|Другие методы:]] == | == [[Методы нахождения экстремумов|Другие методы:]] == | ||
{{Список МНЭ}} | {{Список МНЭ}} | ||
== Ссылки == | == Ссылки == | ||
[[Категория:Математика]][[Категория:Численные методы]][[Категория:Алгоритмы]] | [[Категория:Математика]][[Категория:Численные методы]][[Категория:Алгоритмы]] | ||
Версия 16:14, 15 ноября 2024
Метод дихотомии для оптимизации — это численный метод нахождения экстремума x (с заданной точностью ε), минимизирующего (максимизирующего) функцию f(x) на отрезке.
Содержание
Описание метода
Суть метода дихотомии состоит в разбиении отрезка [a,b] на три отрезка с помощью точек x1 и x2 для определения отрезка содержащего минимальное значение функции f(x).
Деление отрезка продолжается до достижения необходимой точности решения ε.
Сначала находим отрезок [a,b] такой, что функция f(x) непрерывна и вогнута на отрезке, то есть f"(x)>0.
Далее применяем алгоритм.
Алгоритм
Входные данные: f(x), a, b, ε , δ.
Выходные данные: x.
Значение x является минимизирующим решением для функции f(x) с заданной точностью ε.
- Заметим, что для нахождения решения x, максимизирующего выпуклую функцию f(x) на отрезке, алгоритм решения модифицируется в части строки 2, она меняется на строку вида: