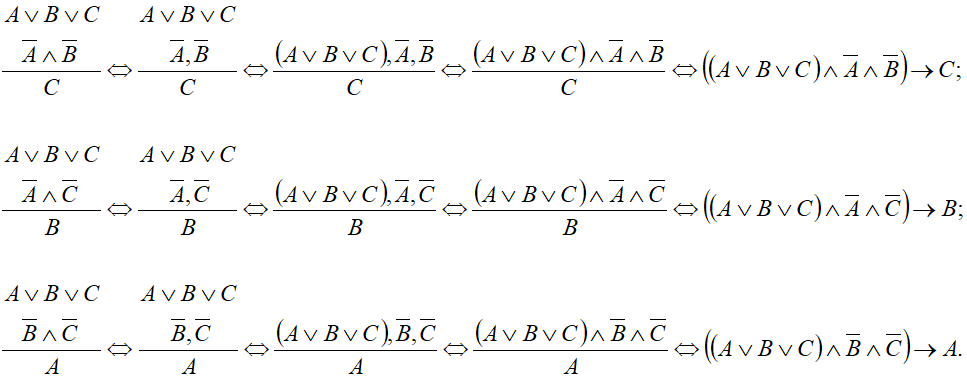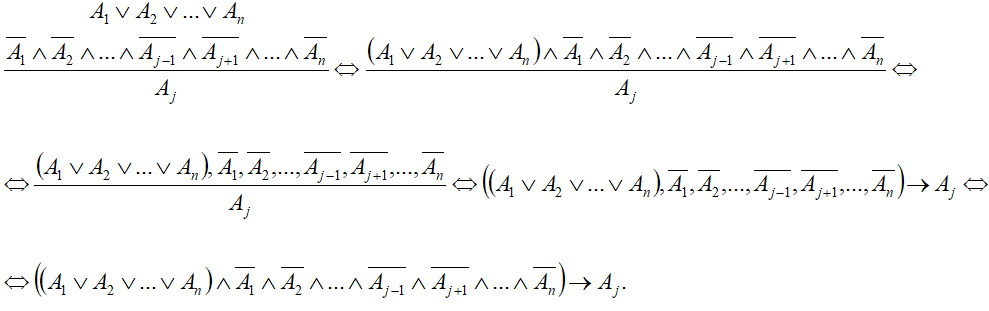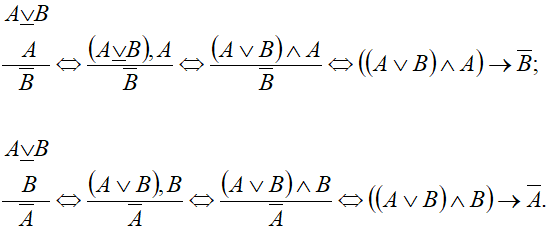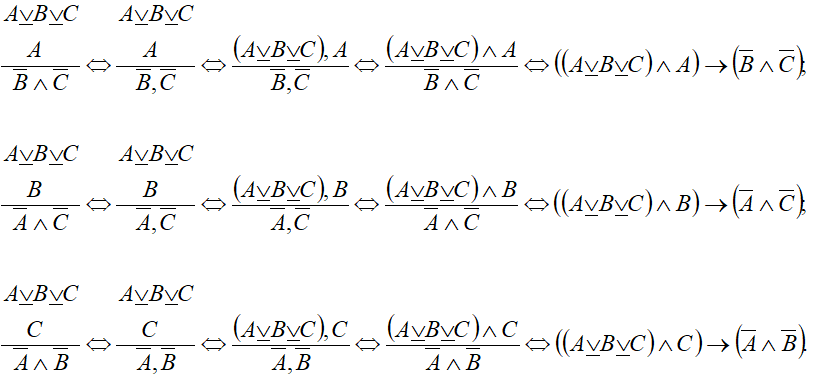Разделительно-категорические умозаключения — различия между версиями
м |
|||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 6: | Строка 6: | ||
== Отрицающе-утверждающий модус == | == Отрицающе-утверждающий модус == | ||
В отрицающее-утверждающем модусе (modus tollendo ponens) меньшая посылка — категорическое суждение — отрицает все члены дизъюнкции, кроме одного, заключение — также категорическое суждение — утверждает оставшийся член дизъюнкции. | В отрицающее-утверждающем модусе (modus tollendo ponens) меньшая посылка — категорическое суждение — отрицает все члены дизъюнкции, кроме одного, заключение — также категорическое суждение — утверждает оставшийся член дизъюнкции. | ||
| + | Большая посылка должна быть дизъюнктивным высказыванием, в ней должны быть перечислены все возможные суждения — дизъюнкты. | ||
=== Дизъюнция 2-х === | === Дизъюнция 2-х === | ||
[[файл:РКУ01.png]] | [[файл:РКУ01.png]] | ||
| Строка 15: | Строка 16: | ||
В утверждающе-отрицающем модусе (modus ponendo tollens) меньшая посылка — категорическое суждение — утверждает один член дизъюнкции, заключение — также категорическое суждение — отрицает все другие её члены. | В утверждающе-отрицающем модусе (modus ponendo tollens) меньшая посылка — категорическое суждение — утверждает один член дизъюнкции, заключение — также категорическое суждение — отрицает все другие её члены. | ||
Заключение по этому модусу достоверно, если соблюдается правило: | Заключение по этому модусу достоверно, если соблюдается правило: | ||
| − | в большей посылке должны быть перечислены все возможные суждения — дизъюнкты, иначе говоря, большая посылка должна быть полным | + | в большей посылке должны быть перечислены все возможные суждения — дизъюнкты, иначе говоря, большая посылка должна быть разделительным (полным, закрытым, строгим) дизъюнктивным высказыванием. |
| − | Применяя неполное | + | Применяя обычное (неполное, открытое, не строгое) дизъюнктивное высказывание, достоверного заключения получить нельзя. |
| − | === | + | === Разделительная дизъюнция 2-х === |
[[файл:РКУ11.png]] | [[файл:РКУ11.png]] | ||
| − | === | + | === Разделительная дизъюнция 3-х === |
[[файл:РКУ12.png]] | [[файл:РКУ12.png]] | ||
| − | === | + | === Разделительная дизъюнция n === |
[[файл:РКУ13.png]] | [[файл:РКУ13.png]] | ||
| − | == [[ | + | == [[Умозаключение|Другие умозаключения:]] == |
| − | {{Список | + | {{Список ЛУмо}} |
== Ссылки == | == Ссылки == | ||
*Википедия | *Википедия | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
| − | [[Категория:Дискретная математика]][[Категория:Логика]] | + | [[Категория:Математика]][[Категория:Дискретная математика]][[Категория:Логика]] |
Текущая версия на 05:08, 21 октября 2024
Разделительно-категорическое умозаключение — это дедуктивное умозаключение, в котором одна из посылок — разделительное, а другая посылка и заключение — категорические суждения.
Содержание
Схема умозаключения
- Большая посылка — дизъюнктивное суждение.
- Меньшая посылка совпадает с одним из членов дизъюнктивного суждения или отрицает все, кроме одного.
- В заключении, соответственно, отрицаются все члены, кроме указанного во второй посылке, или утверждается пропущенный член.
Отрицающе-утверждающий модус
В отрицающее-утверждающем модусе (modus tollendo ponens) меньшая посылка — категорическое суждение — отрицает все члены дизъюнкции, кроме одного, заключение — также категорическое суждение — утверждает оставшийся член дизъюнкции. Большая посылка должна быть дизъюнктивным высказыванием, в ней должны быть перечислены все возможные суждения — дизъюнкты.
Дизъюнция 2-х
Дизъюнция 3-х
Дизъюнция n
Утверждающе-отрицающий модус
В утверждающе-отрицающем модусе (modus ponendo tollens) меньшая посылка — категорическое суждение — утверждает один член дизъюнкции, заключение — также категорическое суждение — отрицает все другие её члены. Заключение по этому модусу достоверно, если соблюдается правило: в большей посылке должны быть перечислены все возможные суждения — дизъюнкты, иначе говоря, большая посылка должна быть разделительным (полным, закрытым, строгим) дизъюнктивным высказыванием. Применяя обычное (неполное, открытое, не строгое) дизъюнктивное высказывание, достоверного заключения получить нельзя.
Разделительная дизъюнция 2-х
Разделительная дизъюнция 3-х
Разделительная дизъюнция n
Другие умозаключения:
Ссылки
- Википедия
- Участник:Logic-samara