Эллипсоид — различия между версиями
(начало) |
м |
||
| Строка 1: | Строка 1: | ||
[[файл:ЭЛТ01.JPG|thumb|300px|Эллипсоид]] | [[файл:ЭЛТ01.JPG|thumb|300px|Эллипсоид]] | ||
| − | '''Эллипсоид''' — | + | '''Эллипсоид''' — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей. |
| − | Является трёхмерным развитием | + | Является трёхмерным развитием эллипса. |
== Обозначения == | == Обозначения == | ||
| Строка 45: | Строка 45: | ||
=== Нормальное уравнение эллипсоида === | === Нормальное уравнение эллипсоида === | ||
: <math>\frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} + \frac{(z-z_0)^2}{c^2} = 1</math> | : <math>\frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} + \frac{(z-z_0)^2}{c^2} = 1</math> | ||
| − | |||
== См.также == | == См.также == | ||
| − | * [[Площадь поверхности эллипсоида]] | + | *[[Площадь поверхности эллипсоида]] |
| − | * [[Объём эллипсоида]] | + | *[[Объём эллипсоида]] |
| − | |||
== Ссылки == | == Ссылки == | ||
| − | * [[Участник:Logic-samara]] | + | *[[Участник:Logic-samara]] |
| − | |||
[[Категория:Математика]][[Категория:Стереометрия]] | [[Категория:Математика]][[Категория:Стереометрия]] | ||
Текущая версия на 08:35, 21 октября 2024
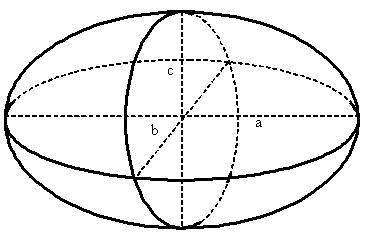
Эллипсоид — поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
Является трёхмерным развитием эллипса.
Содержание
Обозначения
a — первая (большая) полуось;
b — вторая (средняя) полуось;
c — третья (малая) полуось;
p — параметр приближённой формулы;
δ% — относительная ошибка приближённой формулы;
F(k,t) — эллиптический интеграл I рода;
E(k,t) — эллиптический интеграл II рода;
Sэлл — площадь поверхности эллипсоида.
Виды эллипсоида
- трёхосный;
- вытянутый;
- сплюснутый;
- эллипсоид вращения;
- сфера.
Эллипсоид называется трёхосным, если a>b>c.
Эллипсоид называется вытянутым вдоль оси 2a, если a>max{b,c}.
Эллипсоид называется сплюснутым вдоль оси 2c, если c<min{a,b}.
Эллипсоид называется эллипсоидом вращения вокруг оси 2a, если b=c (при a>b является вытянутым).
Эллипсоид называется эллипсоидом вращения вокруг оси 2c, если a=b (при b>с является сплюснутым).
Эллипсоид называется сферой, если a=b=с.
Каноническое уравнение эллипсоида
- <math>\frac{x^2}{a^2} + \frac{y^2}{b^2} + \frac{z^2}{c^2} = 1</math>
Нормальное уравнение эллипсоида
- <math>\frac{(x-x_0)^2}{a^2} + \frac{(y-y_0)^2}{b^2} + \frac{(z-z_0)^2}{c^2} = 1</math>