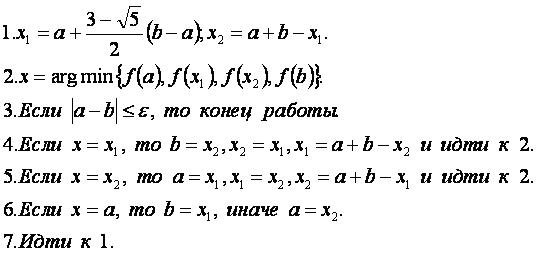Метод золотого сечения
Версия от 15:26, 6 апреля 2023; Logic-samara (обсуждение | вклад)
Метод золотого сечения — это численный метод нахождения решения x (с заданной точностью ε), минимизирующего функцию f(x) на отрезке.
Содержание
Описание метода
Суть метода золотого сечения состоит в разбиении отрезка [a,b] на три отрезка в пропорции золотого сечения, определении минимального значения функции f(x) из значений на границах этих отрезков и выборе нового отрезка, на котором функция содержит минимизирующее решение.
Деление отрезка продолжается до достижения необходимой точности решения ε.
Сначала находим отрезок [a,b] такой, что функция f(x) непрерывна и вогнута на отрезке, то есть f"(x)>0.
Далее применяем алгоритм.
Алгоритм
Входные данные: f(x), a, b, ε.
Выходные данные: x.
Значение x является минимизирующим решением для функции f(x) с заданной точностью ε.
- Заметим, что для нахождения решения x, максимизирующего выпуклую функцию f(x) на отрезке, алгоритм решения модифицируется в части строки 2, она меняется на строку вида:
Другие методы:
Ссылки
- Википедия
- Участник:Logic-samara