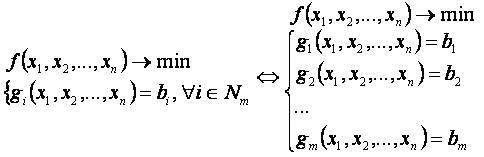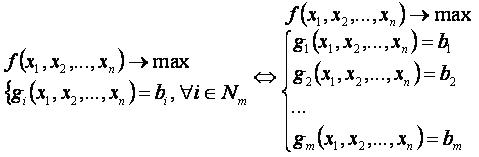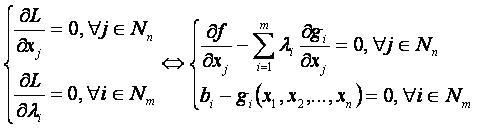Метод множителей Лагранжа
Версия от 15:27, 6 апреля 2023; Logic-samara (обсуждение | вклад)
Метод множителей Лагранжа — это метод нахождения решения x1, x2, …, xn, минимизирующего или максимизирующего функцию f(x1, x2, …, xn) при ограничениях g1(x1, x2, …, xn)=b1, g2(x1, x2, …, xn)=b2, …, gm(x1, x2, …, xn)=bm.
Содержание
Описание метода
Суть метода множителей Лагранжа состоит в построении специальной функции Лагранжа для задачи условной оптимизации, нахождении частных производных и решении системы из этих производных и ограничений.
Задачи условной оптимизации:
- задача условной минимизации;
- задача условной максимизации.
Задача условной минимизации
Задача условной максимизации
Алгоритм
Входные данные: n, m, f(x1, x2, …, xn), g1(x1, x2, …, xn), b1, g2(x1, x2, …, xn), b2, …, gm(x1, x2, …, xn), bm.
1.Составляем функцию Лагранжа:
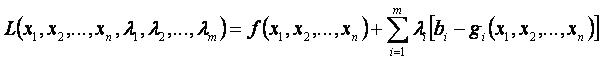
2.Находим частные производные функции Лагранжа по xj и по λi.
4.Из стационарных точек, являющихся решением системы, выбираем оптимальное решение.
Выходные данные: x1, x2, …, xn.
Другие методы:
Ссылки
- Справочник по математике для экономистов. Под ред. проф. В.И.Ермакова. М.: Высшая школа, 1987.
- Участник:Logic-samara