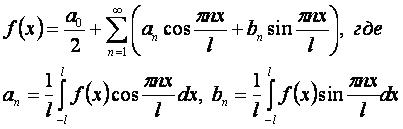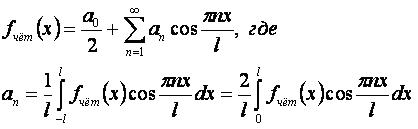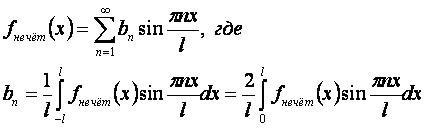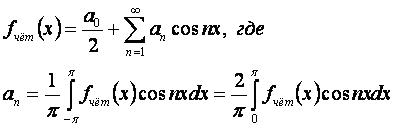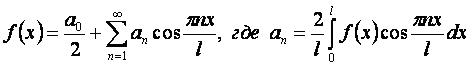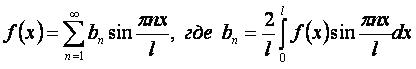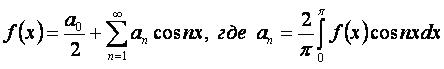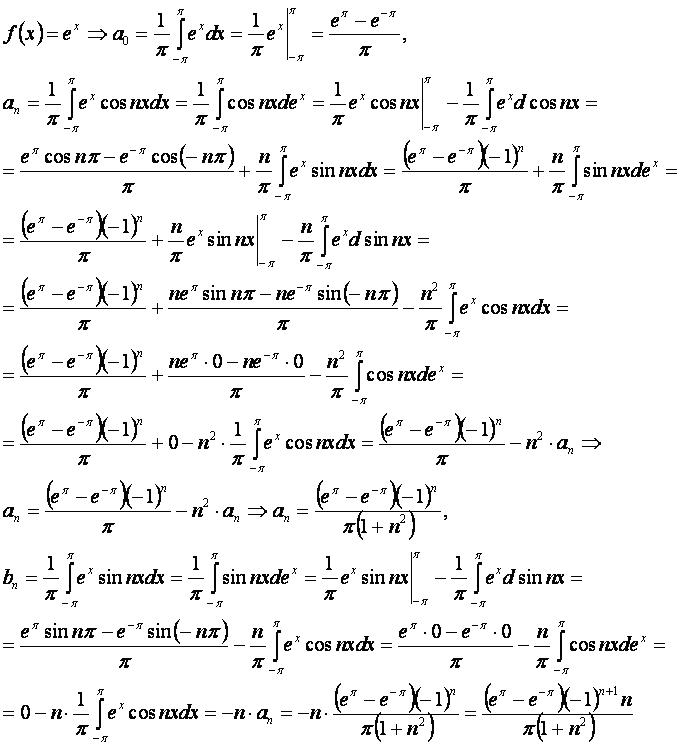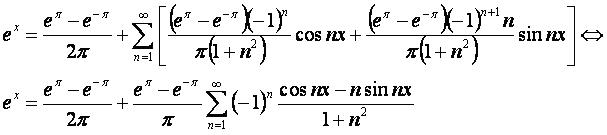Ряд Фурье
Ряд Фурье — это тригонометрический ряд (являющийся разложением функции f(x) на интервале [-l,l]), в котором слагаемыми служат функции ancos(cnx) и bnsin(cnx), а коэффициенты an, bn, cn=πn/l — это числа.
- Периодическая функция f(x) имеет дискретный спектр, т.е. она может быть представлена в виде отдельных гармоник с частотами πn/l.
Содержание
Формулы:
Разложение функции f(x) на интервале [-l,l]:
Разложение функции f(x) на интервале [-π, π]:
Разложение чётной функции fчёт(x) на интервале [-l,l]:
Разложение нечётной функции fнечёт(x) на интервале [-l,l]:
Разложение чётной функции fчёт(x) на интервале [-π, π]:
Разложение нечётной функции fнечёт(x) на интервале [-π, π]:
Разложение функции f(x) по косинусам на интервале [0,l]:
Разложение функции f(x) по синусам на интервале [0,l]:
Разложение функции f(x) по косинусам на интервале [0,π]:
Разложение функции f(x) по синусам на интервале [0,π]:
Пример
Разложение функции f(x)=ex на интервале [-π, π].
Сначала находим коэффициенты:
Окончательно, получаем разложение Фурье:
Другие ряды:
Ссылки
- Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. М.: Наука, 1973.
- Участник:Logic-samara