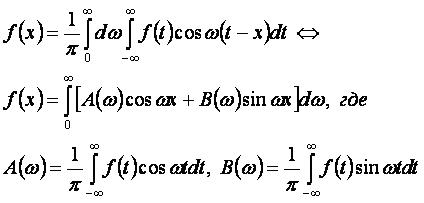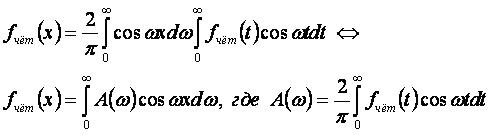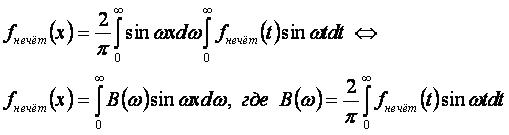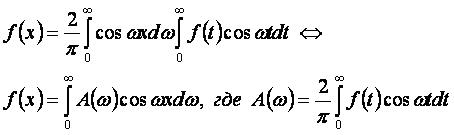Интеграл Фурье — различия между версиями
(начало) |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 22: | Строка 22: | ||
[[файл:ИФУ05.JPG]] | [[файл:ИФУ05.JPG]] | ||
| − | == [[ | + | == [[Математический анализ|Другие интегралы:]] == |
{{Список Инт}} | {{Список Инт}} | ||
== Ссылки == | == Ссылки == | ||
*Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. М.: Наука, 1973. | *Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. М.: Наука, 1973. | ||
| − | + | [[Категория:Математика]][[Категория:Функции]] | |
| − | [[Категория: | ||
Текущая версия на 14:41, 18 февраля 2025
Интеграл Фурье — это представление непериодической функции f(x) в виде интеграла, равного непрерывной сумме гармоник, зависящих от частоты ω на интервале [0,∞).
При этом говорят, что непериодическая функция f(x) имеет непрерывный спектр; частоты образующих её гармоник изменяются непрерывно. Функции A(ω) и B(ω) дают закон распределения амплитуд (и начальных фаз) в зависимости от частоты ω.
Формулы:[править]
Представление функции f(x) на интервале (-∞,∞):
Представление чётной функции fчёт(x) на интервале (-∞,∞):
Представление нечётной функции fнечёт(x) на интервале (-∞,∞):
Представление функции f(x) интегралом с косинусами на интервале [0,∞):
Представление функции f(x) интегралом с синусами на интервале [0,∞):
Другие интегралы:[править]
- интеграл;
- интегралы элементарных функций;
- интегралы дробно-рациональных функций;
- интегралы функций с корнями;
- интегралы тригонометрических функций;
- интегралы обратных тригонометрических функций;
- интегралы гиперболических функций;
- интегралы обратных гиперболических функций;
- интеграл Фурье;
- интеграл Фурье комплексный;
- эллиптические интегралы;
- интегралы, определяемые методом замены переменных;
- интегралы, определяемые по интегральным равенствам;
- интегралы, определяемые по интегральным формулам;
- интеграл Эйлера-Пуассона.
Ссылки[править]
- Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. М.: Наука, 1973.