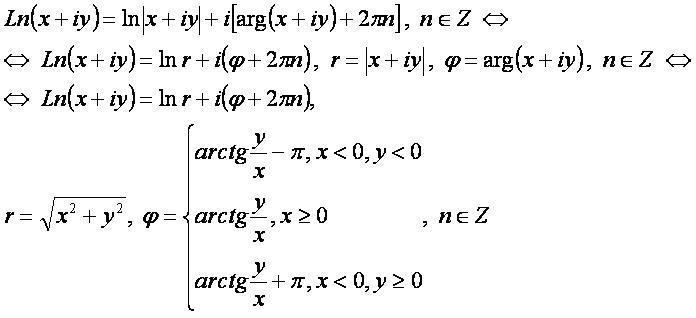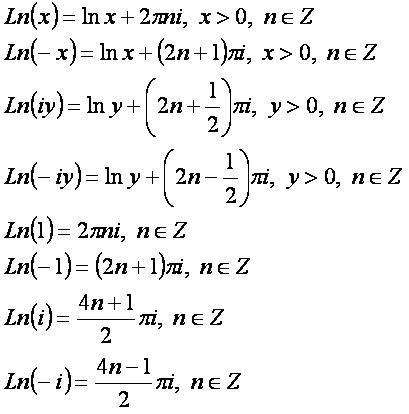Логарифм комплексного числа — различия между версиями
м |
м |
||
| Строка 1: | Строка 1: | ||
'''Логарифм комплексного числа''' – это решение уравнения вида '''e<sup>z</sup>=c''' относительно [[Комплексные числа|комплексной]] переменной '''z'''. | '''Логарифм комплексного числа''' – это решение уравнения вида '''e<sup>z</sup>=c''' относительно [[Комплексные числа|комплексной]] переменной '''z'''. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''x''' — действительная часть (абсцисса) числа; | '''x''' — действительная часть (абсцисса) числа; | ||
| Строка 24: | Строка 22: | ||
== Ссылки == | == Ссылки == | ||
*Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.623. | *Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.623. | ||
| − | + | [[Категория:Математика]][[Категория:Числа]] | |
| − | [[Категория: | ||
Текущая версия на 15:06, 18 февраля 2025
Логарифм комплексного числа – это решение уравнения вида ez=c относительно комплексной переменной z.
Содержание
Обозначения[править]
x — действительная часть (абсцисса) числа;
y — мнимая часть (ордината) числа;
r — модуль комплексного числа;
φ — аргумент комплексного числа;
x+iy — комплексное число;
lnx — натуральный логарифм вещественного числа;
Ln(x+iy) — комплексный натуральный логарифм.
Формула[править]
Примеры:[править]
Другие операции:[править]
- сложение чисел;
- вычитание чисел;
- умножение чисел;
- деление чисел;
- обращение числа;
- возведение в степень;
- извлечение квадратного корня;
- извлечение кубического корня;
- извлечение корня n-ой степени;
- логарифмирование числа;
- возведение в комплексную степень;
- тригонометрические функции комплексных чисел;
- гиперболические функции комплексных чисел;
- взятие комплексно сопряжённого числа;
Ссылки[править]
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.623.