Длина дуги гиперболы

Гипербола

Длина дуги гиперболы — это число, характеризующее протяжённость дуги гиперболы в единицах измерения длины.

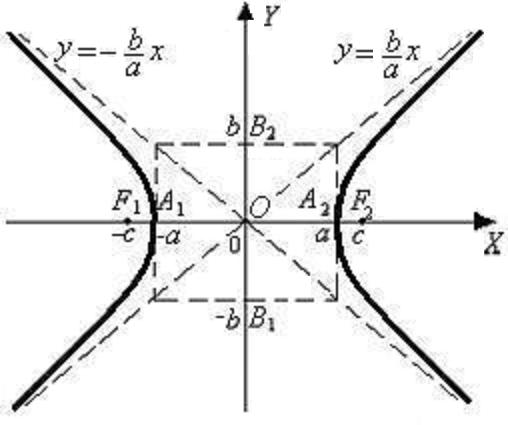
Обозначения

a — действительная полуось;

b — мнимая полуось;

1/k — эксцентриситет;

x²/a²-y²/b²=1 — каноническое уравнение гиперболы;

t₁ — параметр первой точки дуги;

t₂ — параметр второй точки дуги;

t — параметрическая переменная;

x=acht — параметрическое уравнение абсциссы гиперболы;

y=bsht — параметрическое уравнение ординаты гиперболы;

F(k,t) — эллиптический интеграл I рода;

E(k,t) — эллиптический интеграл II рода;

L_{дуг.гип} — длина дуги гиперболы.

Формула

Вывод формулы

• Для вывода используется формула "длина дуги плоской кривой" в параметрической форме.
• Для нахождения интеграла используются эллиптические интегралы I и II рода.

Другие кривые:

• плоская кривая;
• окружность;
• парабола;
• эллипс;
• гипербола;
• синусоида;
• косинусоида;
• циклоида;
• кардиоида;
• астроида;
• эпициклоида;
• гипоциклоида;
• эвольвента;
• цепная линия;
• трактриса;
• лемниската Бернулли.

Ссылки

• Храбров А.И. Немного об эллиптических интегралах. http://www.math.spbu.ru/analysis/f-doska/ellint.pdf