Объём эллипсоида — различия между версиями
(начало) |
м |
||
| Строка 4: | Строка 4: | ||
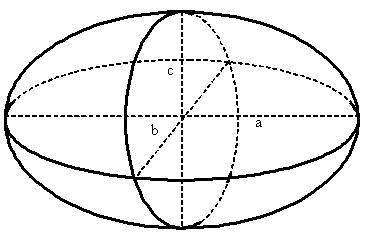
'''Эллипсоид''' (трёхосный) — это [[Объём трёхмерной фигуры|поверхность в трёхмерном пространстве]], полученная деформацией [[Объём шара|сферы]] вдоль трёх взаимно перпендикулярных осей. | '''Эллипсоид''' (трёхосный) — это [[Объём трёхмерной фигуры|поверхность в трёхмерном пространстве]], полученная деформацией [[Объём шара|сферы]] вдоль трёх взаимно перпендикулярных осей. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''a''' — первая (большая) полуось; | '''a''' — первая (большая) полуось; | ||
| Строка 41: | Строка 39: | ||
{{Список ОФТ}} | {{Список ОФТ}} | ||
== Ссылки == | == Ссылки == | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 15:35, 18 февраля 2025
Объём эллипсоида — это число, характеризующее эллипсоид в единицах измерения объёма.
Эллипсоид (трёхосный) — это поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
Обозначения[править]
a — первая (большая) полуось;
b — вторая (средняя) полуось;
c — третья (малая) полуось;
Vэлл — объём эллипсоида.
Виды эллипсоида:[править]
Эллипсоид называется трёхосным, если a>b>c.
Эллипсоид называется вытянутым вдоль оси 2a, если a>max{b,c}.
Эллипсоид называется сплюснутым вдоль оси 2c, если c<min{a,b}.
Эллипсоид называется эллипсоидом вращения вокруг оси 2a, если b=c (при a>b является вытянутым сфероидом).
Эллипсоид называется эллипсоидом вращения вокруг оси 2c, если a=b (при b>с является сплюснутым сфероидом).
Эллипсоид называется сферой, если a=b=с (является нормальным сфероидом).
Формула[править]
- Заметим, что при a=b или b=c формула объёма эллипсоида превращается в формулу объёма сфероида.
Вывод формулы:[править]
- Для вывода используется формула "объём трёхмерной фигуры" в прямоугольных координатах.
- Для нахождения интеграла используется метод замены переменных с переходом к сферическим координатам.