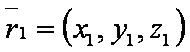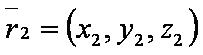Площадь четырёхугольника — различия между версиями
м |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
[[файл:ЧЕТ01.JPG|thumb|300|Четырёхугольник]] | [[файл:ЧЕТ01.JPG|thumb|300|Четырёхугольник]] | ||
| − | '''Площадь четырёхугольника''' — это число, характеризующее четырёхугольник в единицах измерения площади. | + | '''Площадь четырёхугольника''' — это число, характеризующее [[Площадь квадрата|четырёхугольник]] в единицах измерения площади. |
== Определение: == | == Определение: == | ||
'''Плоский выпуклый четырёхугольник''' — это четырёхугольник, у которого все четыре точки (вершины) лежат в одной плоскости и для любых его двух точек (в том числе и вершин) все точки отрезка принадлежат четырёхугольнику. | '''Плоский выпуклый четырёхугольник''' — это четырёхугольник, у которого все четыре точки (вершины) лежат в одной плоскости и для любых его двух точек (в том числе и вершин) все точки отрезка принадлежат четырёхугольнику. | ||
| Строка 13: | Строка 13: | ||
*четырёхугольник. | *четырёхугольник. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''a''' — первая сторона; | '''a''' — первая сторона; | ||
| Строка 96: | Строка 94: | ||
*Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.167. | *Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.167. | ||
*Википедия. Четырёхугольник. | *Википедия. Четырёхугольник. | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 16:07, 18 февраля 2025
Площадь четырёхугольника — это число, характеризующее четырёхугольник в единицах измерения площади.
Содержание
Определение:[править]
Плоский выпуклый четырёхугольник — это четырёхугольник, у которого все четыре точки (вершины) лежат в одной плоскости и для любых его двух точек (в том числе и вершин) все точки отрезка принадлежат четырёхугольнику.
Виды четырёхугольников:[править]
- квадрат;
- прямоугольник;
- ромб;
- параллелограмм;
- трапеция;
- равнобедренная трапеция;
- прямоугольная трапеция;
- четырёхугольник.
Обозначения[править]
a — первая сторона;
b — вторая сторона;
c — третья сторона;
d — четвёртая сторона;
α — угол между сторонами a и b;
β — угол между сторонами b и c;
γ — угол между сторонами c и d;
η — угол между сторонами a и d;
d1 — диагональ, соединяющая вершины углов α и γ;
d2 — диагональ, соединяющая вершины углов β и η;
l1 — средняя линия, соединяющая середины сторон a и c;
l2 — средняя линия, соединяющая середины сторон b и d;
φ — угол (острый) между диагоналями;
ψ — угол (острый) между средними линиями;
p — полупериметр четырёхугольника;
SΔ — площадь треугольника;
Sчетыр — площадь четырёхугольника.
Формулы:[править]
Формулы в векторной и координатной форме[править]
Введём обозначения:
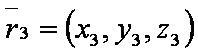
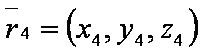
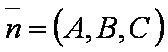
где
Формула Брахмагупты[править]
Рассмотрим четырёхугольники, вокруг которых можно описать окружность и у которых порядок следования вершин 1, 2, 3, 4. Для нахождения их площади можно использовать формулу Брахмагупты.
Введём обозначения:
a — сторона, расположенная между первой и второй точками;
b — сторона, расположенная между второй и третьей точками;
c — сторона, расположенная между третьей и четвёртой точками;
d — сторона, расположенная между первой и четвёртой точками;
p — полупериметр четырёхугольника.
где
- Когда одна из сторон четырёхугольника стремится к нулю, тогда формула Брахмагупты превращается в формулу Герона для площади треугольника.
- Когда четырёхугольник является прямоугольником и a≠b, тогда формула Брахмагупты превращается в формулу площади прямоугольника, Sпрямоуг=ab, где c=a, d=b, p=a+b.
- Когда четырёхугольник является равнобедренной трапецией и b=d, тогда формула Брахмагупты превращается в формулу площади трапеции, Sравн.трап=h(a+c)/2, где h2=(p-a)(p-c), p-b=(a+c)/2.
Другие многоугольники:[править]
Ссылки[править]
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.167.
- Википедия. Четырёхугольник.