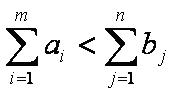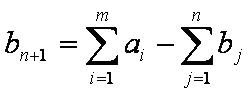Открытая транспортная задача с промежуточными пунктами 2 — различия между версиями
м |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 14: | Строка 14: | ||
'''m-mp''' — число складов с излишками продукции или нулевыми остатками; | '''m-mp''' — число складов с излишками продукции или нулевыми остатками; | ||
| − | '''b<sub>j</sub>>0, j=1,np''' — объём | + | '''b<sub>j</sub>>0, j=1,np''' — объём поставок продукции поставщиков; |
| − | '''b<sub>j</sub><0, j=np+1,n''' — объём | + | '''b<sub>j</sub><0, j=np+1,n''' — объём потребностей (в продукции) потребителей; |
'''a<sub>i</sub>>0, i=1,mp''' — дополнительные (внутренние) потребности продукции (на складе); | '''a<sub>i</sub>>0, i=1,mp''' — дополнительные (внутренние) потребности продукции (на складе); | ||
| Строка 58: | Строка 58: | ||
Для определения начального решения используется '''[[алгоритм северо-западного угла для ТЗПП|метод северо-западного угла]]''', а для решения применяется '''[[Транспортная задача с промежуточными пунктами|метод потенциалов]]'''. | Для определения начального решения используется '''[[алгоритм северо-западного угла для ТЗПП|метод северо-западного угла]]''', а для решения применяется '''[[Транспортная задача с промежуточными пунктами|метод потенциалов]]'''. | ||
Очевидно, что '''M'''-множители и метод потенциалов приводят к нулевым соответствующим (со склада с дополнительными внутренними потребностями к фиктивному потребителю) перевозкам в оптимальном решении. В оптимальном решении вспомогательной задачи все перевозки через конечные (без фиктивного потребителя) и промежуточные пункты являются оптимальным решением исходной задачи. А перевозки к фиктивному потребителю являются не использованными остатками (излишками) складов. | Очевидно, что '''M'''-множители и метод потенциалов приводят к нулевым соответствующим (со склада с дополнительными внутренними потребностями к фиктивному потребителю) перевозкам в оптимальном решении. В оптимальном решении вспомогательной задачи все перевозки через конечные (без фиктивного потребителя) и промежуточные пункты являются оптимальным решением исходной задачи. А перевозки к фиктивному потребителю являются не использованными остатками (излишками) складов. | ||
| − | == Другие задачи: == | + | == [[Транспортные задачи|Другие задачи:]] == |
{{Список ЗТТ}} | {{Список ЗТТ}} | ||
== Ссылки == | == Ссылки == | ||
Текущая версия на 09:16, 21 марта 2025

Открытая транспортная задача с промежуточными пунктами 2 – это открытая транспортная задача оптимизации перевозок с использованием промежуточных (транзитных) пунктов с избытком грузов (для перевозок) в транзитных пунктах.
Содержание
Обозначения:[править]
n — число конечных пунктов (поставщиков и потребителей);
np — число поставщиков;
n-np — число потребителей;
m — число промежуточных пунктов (складов);
mp — число складов с дополнительными (внутренними) потребностями;
m-mp — число складов с излишками продукции или нулевыми остатками;
bj>0, j=1,np — объём поставок продукции поставщиков;
bj<0, j=np+1,n — объём потребностей (в продукции) потребителей;
ai>0, i=1,mp — дополнительные (внутренние) потребности продукции (на складе);
ai≤0, i=mp+1,m — излишки продукции или нулевые остатки (на складе);
cij>0, i=1,m, j=1,np — транспортные тарифы на перевозку единицы продукции от поставщика на склад;
cij<0, i=1,m, j=np+1,n — транспортные тарифы на перевозку единицы продукции со склада к потребителю;
xij≥0, i=1,m, j=1,np — объём перевозок продукции от поставщика на склад;
xij≤0, i=1,m, j=np+1,n — объём перевозок продукции со склада к потребителю.
Математическая модель[править]
- Заметим, что в системе ограничений открытой задачи должно быть хотя бы одно строгое неравенство.
Условия разрешимости[править]
Для разрешимости открытой задачи необходимо выполнение условий:
Введём дополнительные обозначения:
bn+1<0 — объём потребностей (в продукции) фиктивного потребителя;
cin+1≤0, i=1,m — транспортные тарифы на перевозку единицы продукции со склада к фиктивному потребителю;
xin+1≤0, i=1,m — объём перевозок продукции со склада к фиктивному потребителю.
Пусть M — это достаточно большое положительное число.
Для построения вспомогательной эквивалентной закрытой задачи введём фиктивного потребителя с параметрами:
Вспомогательная задача[править]
Решение вспомогательной задачи[править]
Очевидно, что вспомогательная задача является закрытой транспортной задачей с промежуточными пунктами, которая разрешима по построению. Для определения начального решения используется метод северо-западного угла, а для решения применяется метод потенциалов. Очевидно, что M-множители и метод потенциалов приводят к нулевым соответствующим (со склада с дополнительными внутренними потребностями к фиктивному потребителю) перевозкам в оптимальном решении. В оптимальном решении вспомогательной задачи все перевозки через конечные (без фиктивного потребителя) и промежуточные пункты являются оптимальным решением исходной задачи. А перевозки к фиктивному потребителю являются не использованными остатками (излишками) складов.
Другие задачи:[править]
- Транспортная задача;
- Распределительная задача;
- Задача о назначениях;
- Транспортная задача с промежуточными пунктами;
- Транспортная задача с промежуточными пунктами с запретами;
- Транспортная задача с промежуточными пунктами и ограничением по транзиту;
- Открытая транспортная задача с промежуточными пунктами;
- Открытая транспортная задача с промежуточными пунктами 1;
- Открытая транспортная задача с промежуточными пунктами 2;
- Открытая транспортная задача с промежуточными пунктами 3;
- Открытая транспортная задача с промежуточными пунктами 4;
- Трёхиндексная транспортная задача;
- Трёхиндексная транспортная задача с аксиальными суммами;
- Трёхиндексная транспортная задача с промежуточными пунктами.
Ссылки[править]
- Кривопалов В. Ю., Решение открытой транспортной задачи с промежуточными пунктами. Сборник научных трудов конференции ПИТ-2015, СГАУ, Т.2, стр.86-91. http://ssau.ru/files/events/2015/pit_2015_2.pdf
- Участник:Logic-samara