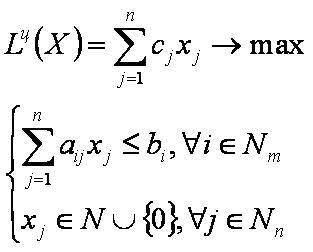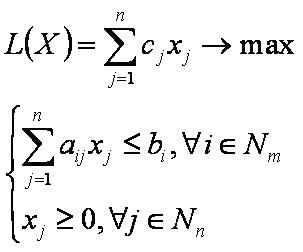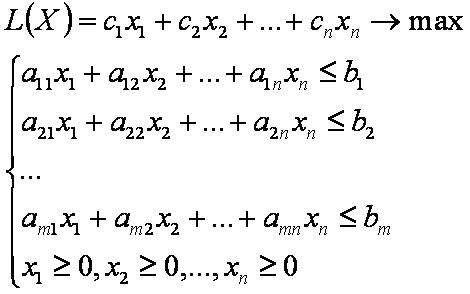Задача целочисленного программирования

Математическая модель ЗЦП

Задача целочисленного программирования — это задача линейного программирования, в которой решение ищется в целых числах.

Математическая модель

Математическая модель задачи целочисленного программирования имеет следующий вид:

или

Метод решения

Задача целочисленного программирования решается методом Гомори. Суть метода состоит в первоначальном решении симплекс-методом вспомогательной задачи линейного программирования (без ограничения целочисленности) вида:

или

.

Затем для нецелочисленной переменной оптимального решения вспомогательной задачи составляется ограничение отсечения и вновь решается вспомогательная задача, но уже М-методом. Причём если в r-ой строке последней симплекс-таблицы базисная переменная не является целочисленной (а она должна быть целочисленной по условию задачи), то составляется ограничение отсечения вида:

, где

{a_rj}=a_rj-[a_rj] - дробная часть числа.

Повторяя процедуру добавления ограничения отсечения и решения вспомогательной задачи, в конце получаем оптимальное целочисленное решение.

Пример решения

Задача целочисленного программирования имеет вид:

Строим вспомогательную задачу линейного программирования (без ограничения целочисленности):

Вспомогательную задачу приводим к каноническому виду:

Решаем первую вспомогательную задачу симплекс-методом:

Составляем первое ограничение отсечения (в ограничении используются десятичные дроби):

Решаем вторую вспомогательную задачу М-методом:

Составляем второе ограничение отсечения (в ограничении используются правильные дроби):

Решаем третью вспомогательную задачу М-методом:

Оптимальное решение последней вспомогательной задачи x₁=5, x₂=2, x₃=0, x₄=7, x₅=4, x₆=1, x₇=0, x₈=0, L=38.

Оптимальное решение задачи целочисленного программирования x₁=5, x₂=2, L^ц =38.

Другие задачи:

• Каноническая задача;
• Производственная задача;
• Общая прямая задача линейного программирования;
• Общая двойственная задача линейного программирования;
• Задачи транспортного типа;
• Задача целочисленного программирования;
• Задача о рюкзаке;
• Задача распределения средств;
• Задача замены оборудования.

Ссылки

• Корбут А.А., Финкельштейн Ю.Ю. Дискретное программирование, «Наука», М., 1969.
• Участник:Logic-samara