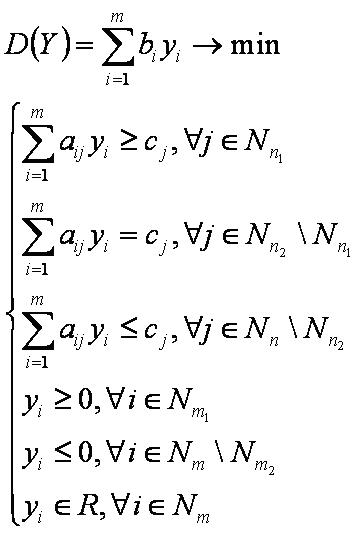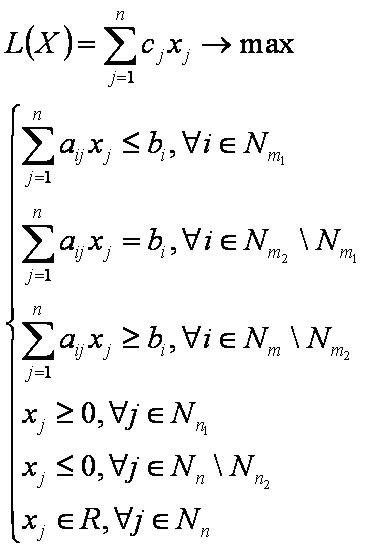Общая двойственная задача линейного программирования

Математическая модель ОДЗ

Общая двойственная задача — это задача минимизации, симметричная общей прямой задаче, с ограничениями всех видов и с переменными всех видов.

Обозначения

m – число переменных;

1, 2, .., m₁ – номера неотрицательных переменных;

m₁+1, m₁+2, …, m₂ – номера переменных без ограничений;

m₂+1, m₂+2, …, m – номера неположительных переменных;

n – число ограничений;

1, 2, .., n₁ – номера ограничений вида ≥;

n₁+1, n₁+2, …, n₂ – номера ограничений вида =;

n₂+1, n₂+2,…, n – номера ограничений вида ≤;

a_ij – коэффициент в j-том ограничении перед i-той переменной;

b_i – коэффициент в целевой функции перед i-той переменной;

c_j – значение границы в j-том ограничении;

y_i – i-тая переменная.

Математическая модель

Математическая модель общей двойственной задачи имеет следующий вид:

или

Построение симметричной задачи

Введём дополнительные переменные:

x_j – j-тая переменная, j=1, 2, .., n.

Соответствия ограничений и переменных двойственной и прямой задач имеют следующий вид:

Симметричная задача

Математическая модель общей прямой задачи имеет следующий вид:

Другие задачи:

• Каноническая задача;
• Производственная задача;
• Общая прямая задача линейного программирования;
• Общая двойственная задача линейного программирования;
• Задачи транспортного типа;
• Задача целочисленного программирования;
• Задача о рюкзаке;
• Задача распределения средств;
• Задача замены оборудования.

Ссылки

• Юдин Д.Б., Гольштейн Е.Г. Линейное программирование., М.,1963.