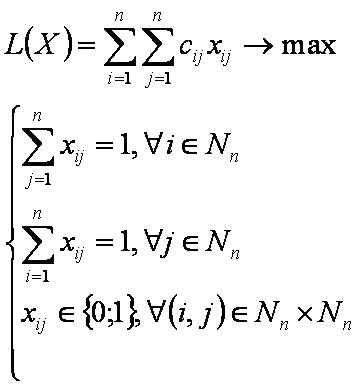Задача о назначениях — различия между версиями
м |
|||
| Строка 32: | Строка 32: | ||
*Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа, М.,1969. | *Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа, М.,1969. | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
| − | [[Категория:Линейное программирование]][[Категория:Транспортная задача]][[Категория:Логистика]] | + | [[Категория:Математика]][[Категория:Линейное программирование]][[Категория:Транспортная задача]][[Категория:Логистика]] |
Текущая версия на 15:17, 6 апреля 2023
Задача о назначениях – это задача оптимального назначения работ исполнителям.
Содержание
[скрыть]Постановка задачи
Пусть имеется n работ (A1,A2,…,An) и n исполнителей (B1,B2,…,Bn). Пусть известны доходы cij от назначения i-ой работы j-ому исполнителю и необходимо определить назначения с наибольшей суммой доходов, при этом каждая работа назначается только одному исполнителю и каждый исполнитель назначается только на одну работу. Тогда задача о назначениях (ЗН) формулируется следующим образом:
,
где xij – 1 если есть назначение i-ой работы j-ому исполнителю, 0 - если нет назначения.
Метод решения
Задача о назначениях решается венгерским методом.
Пример ЗН
Подготовительный этап
Решение венгерским методом
Оптимальное решение равно
Другие задачи:
- Транспортная задача;
- Распределительная задача;
- Задача о назначениях;
- Транспортная задача с промежуточными пунктами;
- Транспортная задача с промежуточными пунктами с запретами;
- Транспортная задача с промежуточными пунктами и ограничением по транзиту;
- Открытая транспортная задача с промежуточными пунктами 1;
- Открытая транспортная задача с промежуточными пунктами 2;
- Открытая транспортная задача с промежуточными пунктами 3;
- Открытая транспортная задача с промежуточными пунктами 4;
- Трёхиндексная транспортная задача.
Ссылки
- Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа, М.,1969.
- Участник:Logic-samara
