Длина дуги лемнискаты Бернулли

Лемниската Бернулли

Длина дуги лемнискаты Бернулли — это число, характеризующее протяжённость дуги лемнискаты Бернулли в единицах измерения длины.

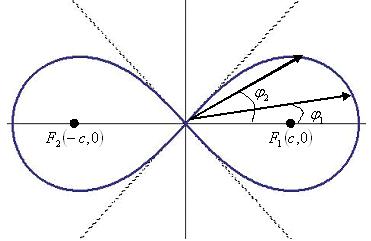
Лемниската Бернулли — это геометрическое место точек, произведение расстояний от которых до фокусов ((-c,0) и (c,0)) постоянно и равно квадрату половины расстояния между фокусами (c²).

Обозначения

F₁ — правый фокус;

F₂ — левый фокус;

c — половина расстояния между фокусами;

(x²+y²)²=2c²(x²-y²) — уравнение лемнискаты Бернулли;

φ₁ — угол (меньший) первой точки дуги;

φ₂ — угол (больший) второй точки дуги;

φ — независимая переменная;

r²=2c²cos2φ — уравнение лемнискаты Бернулли в полярных координатах;

t₁ — параметр первой точки дуги;

t₂ — параметр второй точки дуги;

t — вспомогательная параметричиская переменная;

F(k,t) — эллиптический интеграл I рода;

L_{дуг.лемн} — длина дуги лемнискаты Бернулли.

Формула

• Периметр лемнискаты Бернулли (из двух лепестков) равен P_лемн=4cF(√2/2,π/2).

Вывод формулы

• Для вывода используется формула "длина дуги плоской кривой" в полярных координатах.
• Для нахождения интеграла используется эллиптический интеграл I рода.

Другие кривые:

• плоская кривая;
• окружность;
• парабола;
• эллипс;
• гипербола;
• синусоида;
• косинусоида;
• циклоида;
• кардиоида;
• астроида;
• эпициклоида;
• гипоциклоида;
• эвольвента;
• цепная линия;
• трактриса;
• лемниската Бернулли.

Ссылки

• Храбров А.И. Немного об эллиптических интегралах. http://www.math.spbu.ru/analysis/f-doska/ellint.pdf