Площадь параллелограмма — различия между версиями
м |
м |
||
| Строка 4: | Строка 4: | ||
'''Параллелограмм''' — это [[Площадь четырёхугольника|четырёхугольник]] у которого противоположные стороны равны и параллельны. | '''Параллелограмм''' — это [[Площадь четырёхугольника|четырёхугольник]] у которого противоположные стороны равны и параллельны. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''a''' — большая сторона (основание); | '''a''' — большая сторона (основание); | ||
| Строка 47: | Строка 45: | ||
{{Список ПМУ}} | {{Список ПМУ}} | ||
== Ссылки == | == Ссылки == | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 16:08, 18 февраля 2025
Площадь параллелограмма — это число, характеризующее параллелограмм в единицах измерения площади.
Параллелограмм — это четырёхугольник у которого противоположные стороны равны и параллельны.
Содержание
Обозначения[править]
a — большая сторона (основание);
b — меньшая сторона (боковая);
h — меньшая высота (опущенная на основание);
H — большая высота (опущенная на боковую сторону);
α — острый (меньший) угол между сторонами;
β — тупой (больший) угол между сторонами (β=π-α);
γ — острый (меньший) угол между диагоналями;
d1 — большая диагональ (из угла α);
d2 — меньшая диагональ (из угла β);
Sпар — площадь параллелограмма.
Формулы:[править]
Формулы в векторной и координатной форме[править]
Введём обозначения:
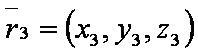
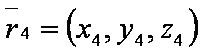
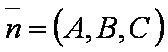
p — отклонение начала координат от плоскости, проходящей через заданные точки.
- Формула с параметром p применима, только когда p≠0.