Шестнадцатеричная система счисления — различия между версиями
м |
м |
||
| Строка 26: | Строка 26: | ||
=== Таблица умножения в десятичной системе счисления === | === Таблица умножения в десятичной системе счисления === | ||
[[файл:ТУ1016.png]] | [[файл:ТУ1016.png]] | ||
| − | == Таблица тетрад == | + | == Таблица 4-ичных пар == |
| − | [[файл:ТТ216. | + | [[файл:ТТ216.png]] |
| + | == Таблица 2-ичных тетрад == | ||
| + | [[файл:ТТ216.png]] | ||
== Примеры алгоритмов: == | == Примеры алгоритмов: == | ||
=== [[Перевод чисел из шестнадцатеричной системы счисления в двоичную]] === | === [[Перевод чисел из шестнадцатеричной системы счисления в двоичную]] === | ||
Версия 05:10, 14 октября 2023
Шестнадцатеричная система (16-ричная система) — позиционная система счисления с основанием 16.
Содержание
Обозначения:
Введём обозначения:
a16 – натуральное число в шестнадцатеричной системе счисления;
a10 – натуральное число в десятичной системе счисления;
n – число цифр в числе a16;
bj_16 – j-тая (справа-налево) шестнадцатеричная цифра числа a16, принимает значения цифр от 0 до 9 и латинских букв от A до F;
bj_10 – десятичное число соответствующее j-той (справа-налево) шестнадцатеричной цифре числа a16, принимает значения от 0 до 15. Буквы A, B, C, D, E, F имеют значения 1010, 1110, 1210, 1310, 1410, 1510 соответственно.
Формула числа
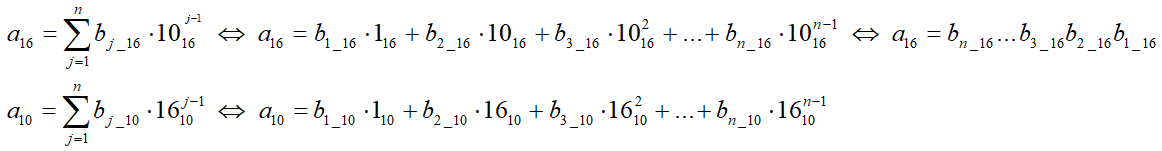 С помощью n позиций в шестнадцатеричной системе счисления можно записать целые числа в диапазоне от 0 до 16n-1, то есть всего 16n различных чисел.
С помощью n позиций в шестнадцатеричной системе счисления можно записать целые числа в диапазоне от 0 до 16n-1, то есть всего 16n различных чисел.
Таблицы сложения:
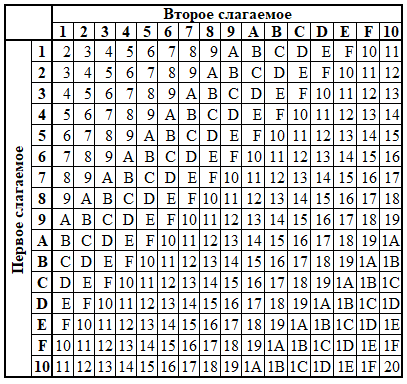
Таблица сложения в шестнадцатеричной системе счисления
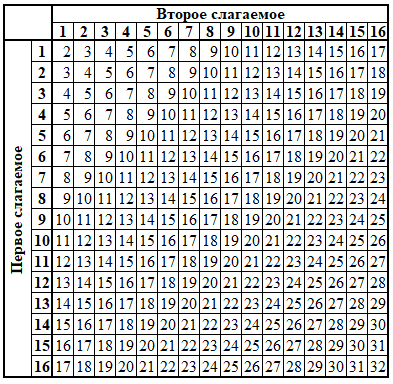
Таблица сложения в десятичной системе счисления
Таблицы умножения:
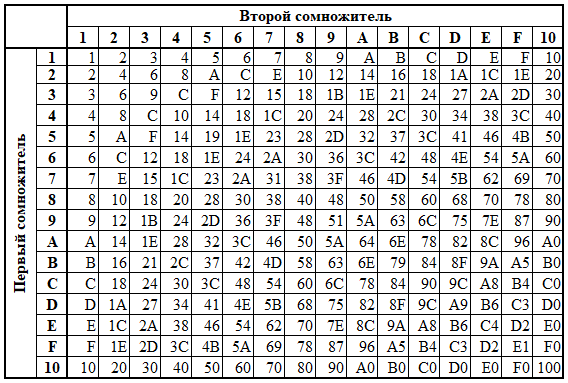
Таблица умножения в шестнадцатеричной системе счисления
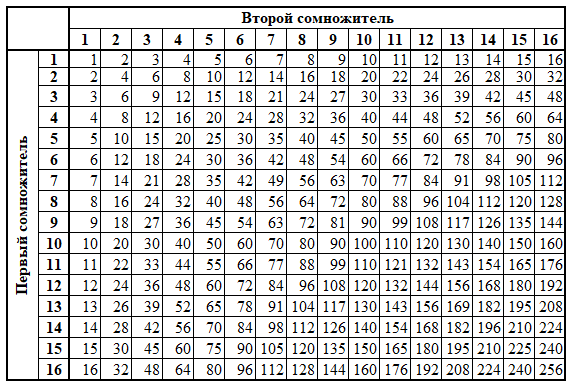
Таблица умножения в десятичной системе счисления
Таблица 4-ичных пар
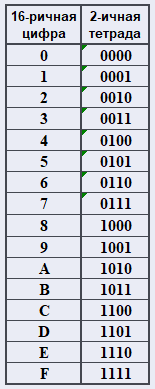
Таблица 2-ичных тетрад
Примеры алгоритмов:
Перевод чисел из шестнадцатеричной системы счисления в двоичную
Цифры исходного числа шестнадцатеричной системы счисления заменяются (слева направо) на соответствующие (по таблице тетрад) тетрады (четвёрки цифр двоичной системы счисления). Незначащие нули первой (самой левой) тетрады опускаются (отбрасываются).
Пример перевода 16→2
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Исходное число двоичной системы счисления разбивается на тетрады (четвёрки цифр двоичной системы счисления), начиная с цифры единиц (самой правой). Последняя (самая левая) тетрада может быть неполной, тогда в неё слева добавляется цифра 0 (одна, две или три). Затем тетрады заменяются на соответствующие (по таблице тетрад) цифры шестнадцатеричной системы счисления.
Пример перевода 2→16
Другие системы счисления:
- двоичная (цифры:0-1);
- троичная (цифры:0-2);
- четверичная (цифры:0-3);
- пятеричная (цифры:0-4);
- шестеричная (цифры:0-5);
- семеричная (цифры:0-6);
- восьмеричная (цифры:0-7);
- девятеричная (цифры:0-8);
- десятичная (цифры:0-9);
- одиннадцатиричная (цифры:0-9,A);
- одиннадцатиричная специальная (цифры:0-9,A);
- двенадцатеричная (цифры:0-9,A-B);
- тринадцатеричная (цифры:0-9,A-C);
- четырнадцатеричная (цифры:0-9,A-D);
- пятнадцатеричная (цифры:0-9,A-E);
- шестнадцатеричная (цифры:0-9,A-F).