Длина дуги трактрисы

Трактриса

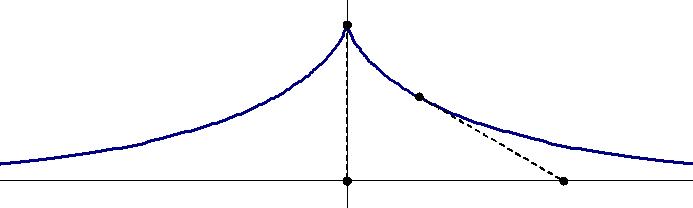
Длина дуги трактрисы — это число, характеризующее протяжённость дуги трактрисы в единицах измерения длины.

Трактриса — это линия, исходящая из вершины M₀ в обе стороны, описываемая точкой M, увлекаемой нерастяжимой нитью LM длиной R, при движении точки L по направляющей (оси абсцисс).

Рассмотрим дуги трактрисы, исходящей из точки (0,R).

Обозначения

x₁ — абсцисса (меньшая) первой точки;

y₁ — ордината первой точки;

t₁ — параметр (меньший) первой точки;

x₂ — абсцисса (большая) второй точки;

y₂ — ордината второй точки;

t₂ — параметр (больший) второй точки;

R — высота трактрисы;

L — точка оси абсцисс, являющейся направляющей;

M=(x,y) — точка трактрисы;

M₀=(0,R) — вершина трактрисы;

t — параметрическая переменная (угол наклона трактрисы);

x=R[cost+lntg(t/2)] — параметрическое уравнение абсциссы трактрисы;

y= Rsint — параметрическое уравнение ординаты трактрисы;

L_{дуг.трак} — длина дуги трактрисы.

Формула

• Длина дуги трактрисы M₀M от вершины равна L_t=-Rln|sint|.

Вывод формулы

• Для вывода используется формула "длина дуги плоской кривой" в параметрической форме.

Другие кривые:

• плоская кривая;
• окружность;
• парабола;
• эллипс;
• гипербола;
• синусоида;
• косинусоида;
• циклоида;
• кардиоида;
• астроида;
• эпициклоида;
• гипоциклоида;
• эвольвента;
• цепная линия;
• трактриса;
• лемниската Бернулли.

Ссылки

• Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.114.
• Выгодский М.Я. Справочник по высшей математике. М.: Наука, 1964, стр.822.