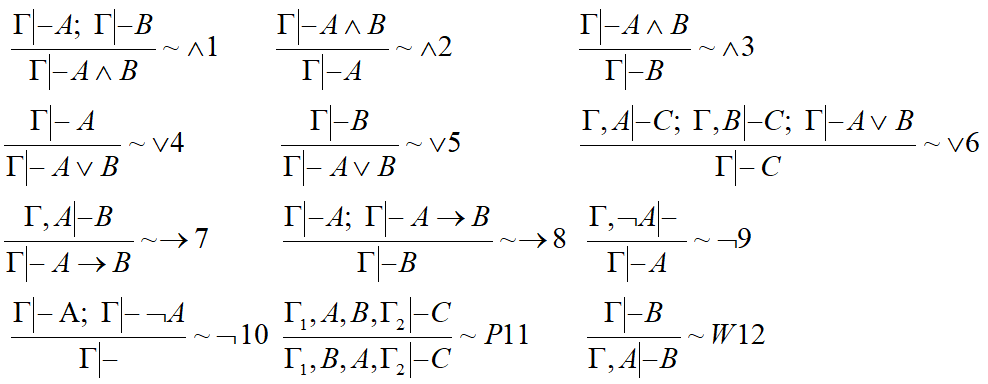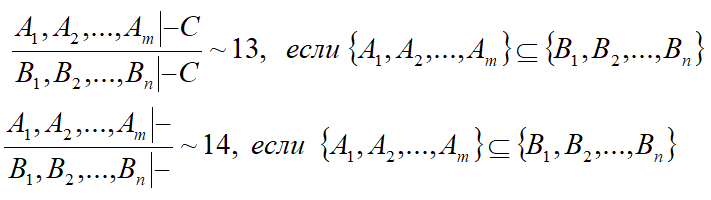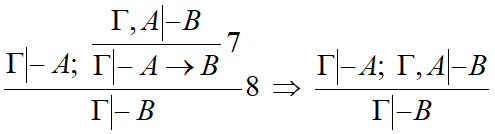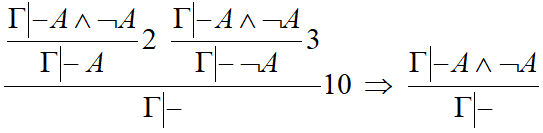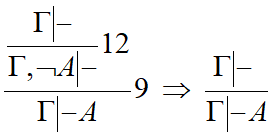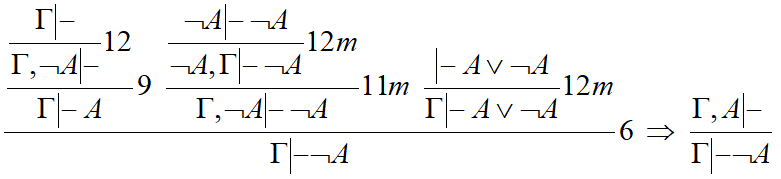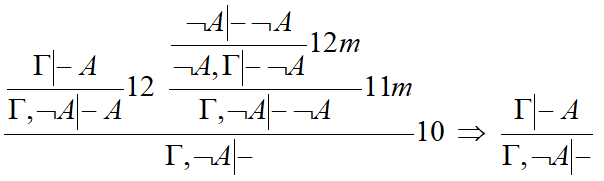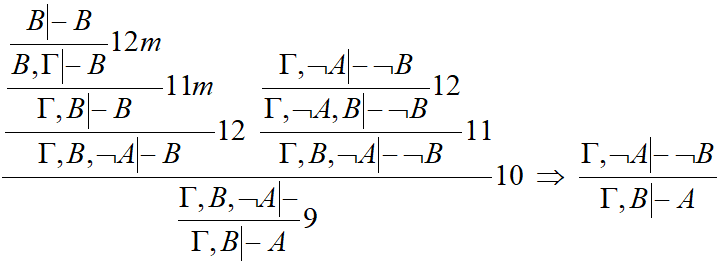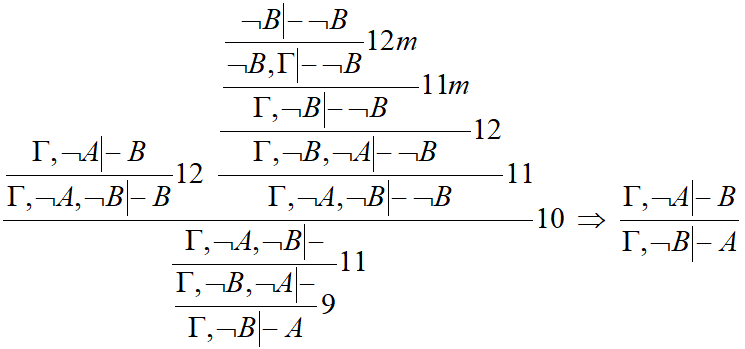Специальное исчисление высказываний — различия между версиями

Версия 13:11, 4 апреля 2025

Специальное исчисление высказываний (секвенций) — построение логической последовательности условных суждений (секвенций) по определённым правилам. В секвенциальном подходе используется аксиома и правила вывода, а доказательство ведётся в форме дерева вывода. Исчисления секвенций относятся к генценовскому типу.

Обозначения

A, B, C — одиночные формулы;

Γ, Г₁, Г₂ — списки формул антецедента, возможно пустые;

A₁, A₂, …, A_n — формулы списка антецедента;

B₁, B₂, …, B_m — формулы списка антецедента;

Ø — пустое множество формул;

├ — знак вывода;

W –– ослабление;

P –– перестановка;

˄ –– конъюнкция;

˅ –– дизъюнкция;

¬ –– отрицание;

→ –– импликация.

Определения

Секвенции (латинское sequentia — последовательность, следствие) — это выражения вида A₁, A₂,..., A_m |- B₁, B₂,..., B_n, где |- — знак выводимости, A₁, A₂,..., A_m и B₂,..., B_n — произвольные формулы; первые — образующие антецедент секвенции, вторые — её сукцедент. Такого рода выражения изучаются в теории доказательств. Они оказываются более удобными для анализа синтаксической структуры выводов. Их называют исчислениями генценовского типа (по имени Генцена, который начал их изучать).