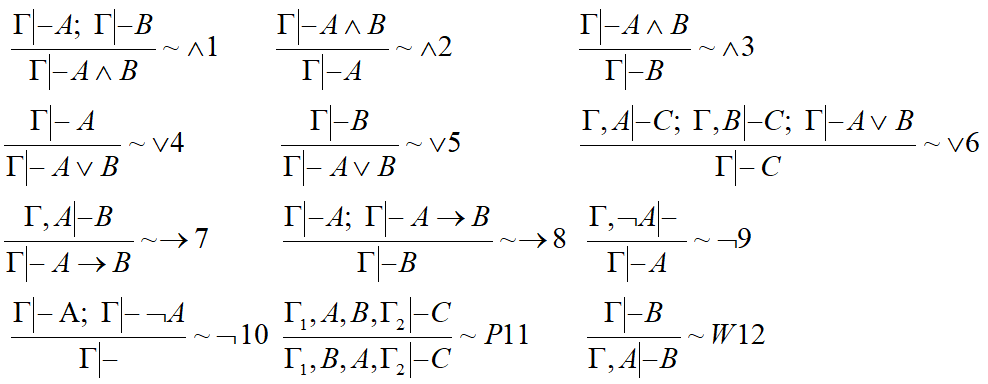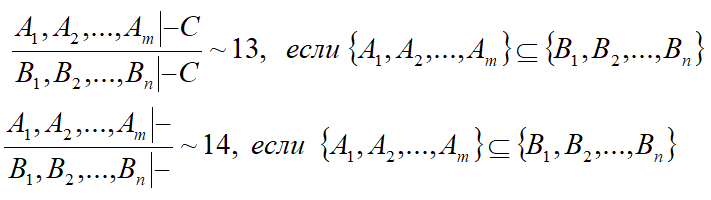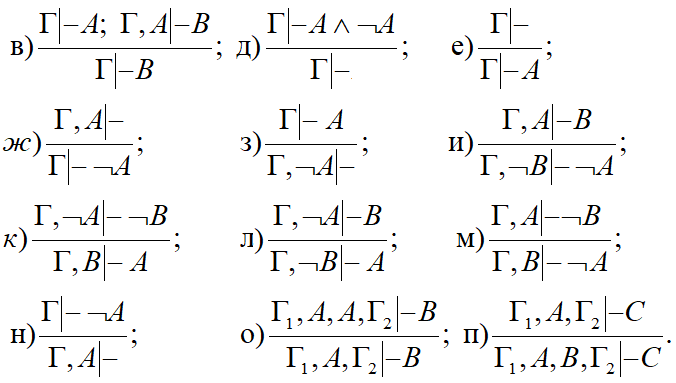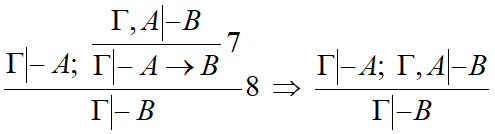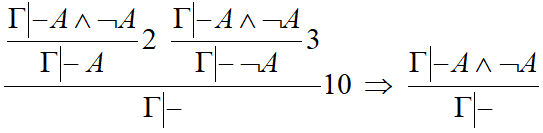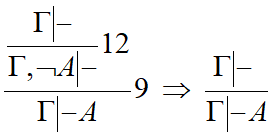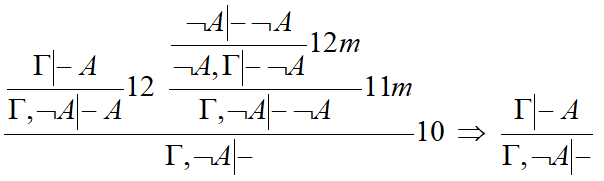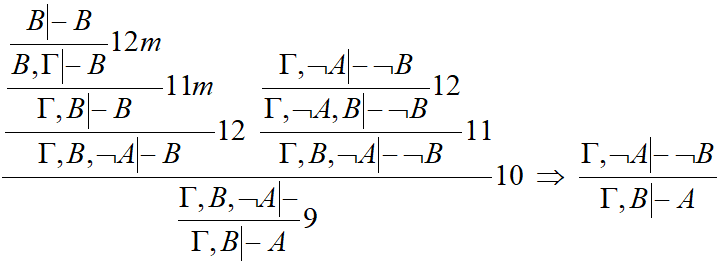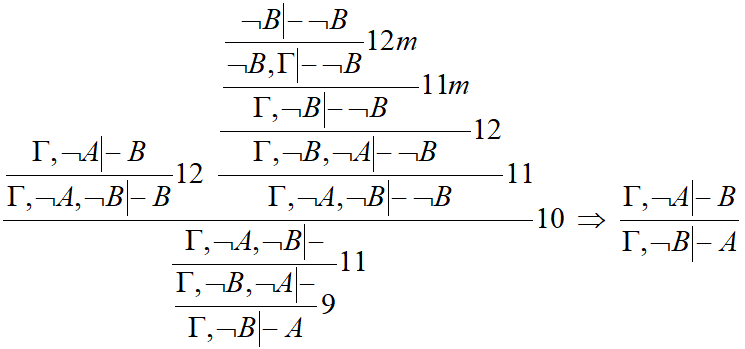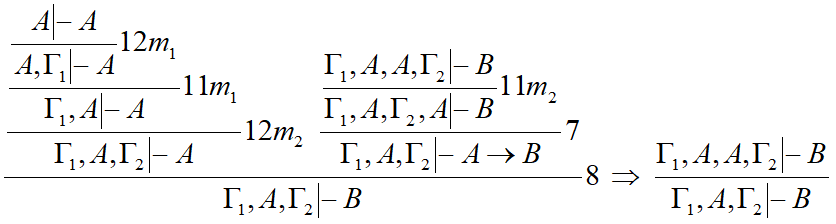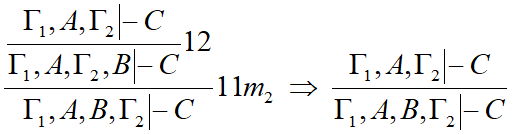Специальное исчисление высказываний — различия между версиями
м |
м |
||
| Строка 53: | Строка 53: | ||
<!--[[файл:СЕК30з.JPG]]--> | <!--[[файл:СЕК30з.JPG]]--> | ||
[[файл:СИВ25.png]] | [[файл:СИВ25.png]] | ||
| − | === '''Пример_и''' === | + | <!--=== '''Пример_и''' === |
[[файл:СЕК30и.JPG]] | [[файл:СЕК30и.JPG]] | ||
| − | [[файл:СИВ26.png]] | + | [[файл:СИВ26.png]]--> |
=== '''Пример_к''' === | === '''Пример_к''' === | ||
<!--[[файл:СЕК30к.JPG]]--> | <!--[[файл:СЕК30к.JPG]]--> | ||
Текущая версия на 16:44, 5 апреля 2025
Специальное исчисление высказываний (секвенций) — построение логической последовательности условных суждений (секвенций) по определённым правилам. В секвенциальном подходе используется аксиома и правила вывода, а доказательство ведётся в форме дерева вывода. Исчисления секвенций относятся к генценовскому типу.
Содержание
Обозначения[править]
A, B, C — одиночные формулы;
Γ, Г1, Г2 — списки формул антецедента, возможно пустые;
A1, A2, …, Am — формулы списка антецедента;
B1, B2, …, Bn — формулы списка антецедента;
Ø — пустое множество формул;
├ — знак вывода;
W –– ослабление;
P –– перестановка;
˄ –– конъюнкция;
˅ –– дизъюнкция;
¬ –– отрицание;
→ –– импликация.
Определения[править]
Секвенции (латинское sequentia — последовательность, следствие) — это выражения вида A1, A2,..., Am |- B1, B2,..., Bn, где |- — знак выводимости, A1, A2,..., Am и B2,..., Bn — произвольные формулы; первые — образующие антецедент секвенции, вторые — её сукцедент. Такого рода выражения изучаются в теории доказательств. Они оказываются более удобными для анализа синтаксической структуры выводов. Их называют исчислениями генценовского типа (по имени Генцена, который начал их изучать).
Аксиома[править]
Основные правила[править]
Дополнительные правила[править]
Примеры секвенций[править]
Доказательства секвенций[править]
Пример_в[править]
Пример_д[править]
Пример_е[править]
Пример_з[править]
Пример_к[править]
Пример_л[править]
Пример_о[править]
Пример_п[править]
Другие понятия:[править]
Ссылки[править]
- Генцен Г. Исследования логических выводов. В кн. Математическая теория логического вывода, М, 1967, с. 9—74.
- Участник:Logic-samara