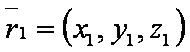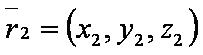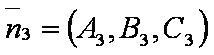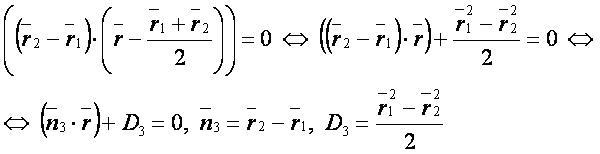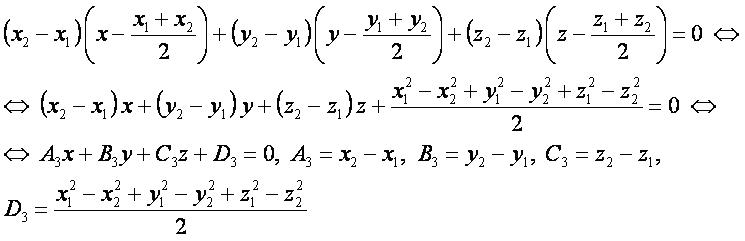Уравнение плоскости, равноудалённой от двух точек — различия между версиями
(начало) |
м |
||
| Строка 3: | Строка 3: | ||
Введём обозначения: | Введём обозначения: | ||
| − | [[файл: | + | [[файл:ВЕК79.JPG]] — радиус-[[вектор]] точки плоскости; |
| − | [[файл: | + | [[файл:ВЕК71.JPG]] — радиус-вектор первой точки; |
| − | [[файл: | + | [[файл:ВЕК72.JPG]] — радиус-вектор второй точки; |
| − | [[файл: | + | [[файл:ВЕК93.JPG]] — нормаль к плоскости; |
[[файл:ПЛО03.JPG]] — уравнение плоскости. | [[файл:ПЛО03.JPG]] — уравнение плоскости. | ||
Версия 14:37, 8 февраля 2021
Будем считать, что плоскость, равноудалённая от двух точек, – это плоскость, все точки которой одинаково удалены от заданных точек. Тогда эта плоскость проходит через середину отрезка между точками перпендикулярно этому отрезку.
Содержание
Обозначения
Введём обозначения:
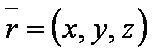
Формулы:
Векторная форма:
Координатная форма:
Другие уравнения:
- уравнение плоскости, проходящей через три точки;
- уравнение плоскости, равноудалённой от двух точек;
- уравнение плоскости, равноудалённой от двух прямых;
- уравнение плоскости, проходящей через две точки параллельно прямой;
- уравнение плоскости, проходящей через две точки перпендикулярно плоскости;
- уравнение плоскости, проходящей через точку и прямую;
- уравнение плоскости, проходящей через точку перпендикулярно прямой;
- уравнение плоскости, проходящей через точку параллельно плоскости;
- уравнение плоскости, проходящей через точку параллельно двум прямым;
- уравнение плоскости, проходящей через точку перпендикулярно двум плоскостям;
- уравнение плоскости, проходящей через прямую параллельно прямой;
- уравнение плоскости, проходящей через прямую перпендикулярно плоскости.