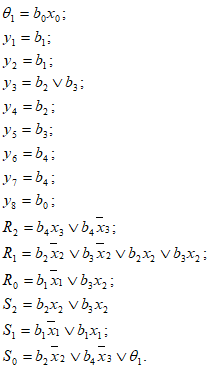Синтез автомата Мура по граф-схеме

Синтез автомата Мура по граф-схеме — это метод построения функциональной схемы автомата.

Описание

Определение 1

Автомат Мура — абстрактный автомат второго рода — конечный автомат, выходное значение сигнала в котором зависит лишь от текущего состояния данного автомата, и, не зависит напрямую, в, отличие от автомата Мили, от входных значений. Автомат Мура назван в честь описавшего его свойства Эдварда Ф. Мура, опубликовавшего исследования в 1956 году в издании «Gedanken-experiments on Sequential Machines.».

Определение 2

Автомат Мура — кортеж из 6 элементов, включающий: множество внутренних состояний S (внутренний алфавит); начальное состояние S0; множество входных сигналов X (входной алфавит); множество выходных сигналов Y (выходной алфавит); функция переходов.

Обозначения

ГСА — граф-схема автомата;

ФСА — функциональная схема автомата;

b₀ — операторная вершина — начальное и конечное состояние автомата;

b_m — операторная вершина — исходное состояние перехода;

ө_s' — узел — дополнительная операторная вершина для упрощения ГСА;

b_m→b_s — переход из одной операторной вершины в другую;

b_m→ө_s, ө_m→b_s, ө_m→ө_s — дополнительные переходы;

X(b_m, b_s) — логическое условие перехода;

S_i' — S-триггер;

R_i' — R-триггер.

Пример 1

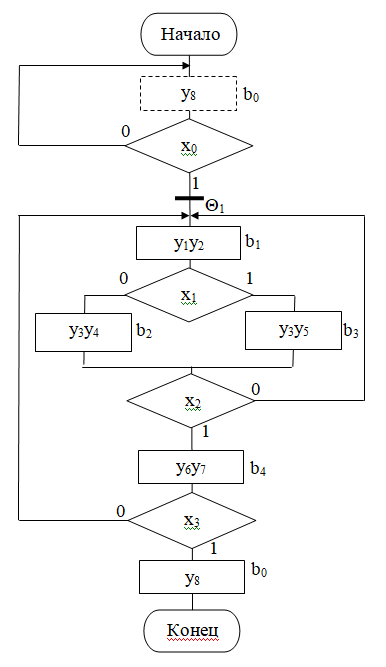
Синтез автомата Мура по ГСА (рис.1).

Рис.1. ГСА автомата Мура с узлами.

1) Разметка состояний. В автомате Мура каждой операторной вершине соответствует состояние автомата. Переход из состояния bm в состояние bs — это переход из одной операторной вершины в другую при выполнении логический условий X(bm,bs) на пути из bm в bs. Т.к. начальное и конечное состояние автомата совпадают, на ГСА искусственно добавлена еще одна операторная вершина, соответствующая состоянию b0. Узлы ө используются для упрощения формул переходов и ставятся на ГСА в точках, где несколько путей сходятся, а затем расходятся. Узлы не кодируются.

Рис.2. Размеченная ГСА автомата Мура с узлами.

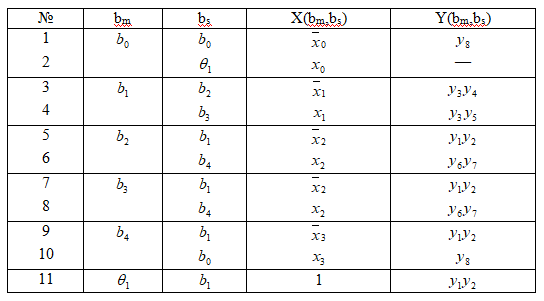
2) Построение прямой таблицы переходов 1. Отличительная особенность: в данном примере в ГСА введены узлы ө. В ГСА с узлами возможны переходы четырех видов: b_m→b_s, b_m→ө_s, ө_m→b_s, ө_m→ө_s. Все эти переходы описываются в прямой таблице переходов.

Таблица 1.

В столбце X(bm,bs) единица записывается тогда, когда b_m в b_s переход осуществляется всегда. 3) Кодирование состояний. Произведём кодирование узлов (узлы ө не кодируются). В данном примере — автомат имеет четыре состояния (кроме начального), для кодирования необходимо не менее трёх двоичных разрядов. Память состояний на RS триггерах. Коды состояний: k(b₀)=000; k(b₁)=001; k(b₂)=010; k(b₃)=011; k(b₄)=100. 4) Построение обратной структурной таблицы 2. Вначале описываем переходы в узлы, затем остальные переходы автомата.

Таблица 2.

Если переход в некоторое состояние b_s происходит из узла ө, то в автомате с памятью на RS триггерах значения R_i и S_i в обратной структурной таблице записываются с учетом кодов состояний b_m из которых был переход в узел ө.

Рис.3. Схема определения значений R_i и S_i.

5) Запись функции выходов и переходов автомата. По обратной структурной таблице запишем функции для ө, Y_i, R_i и S_i.

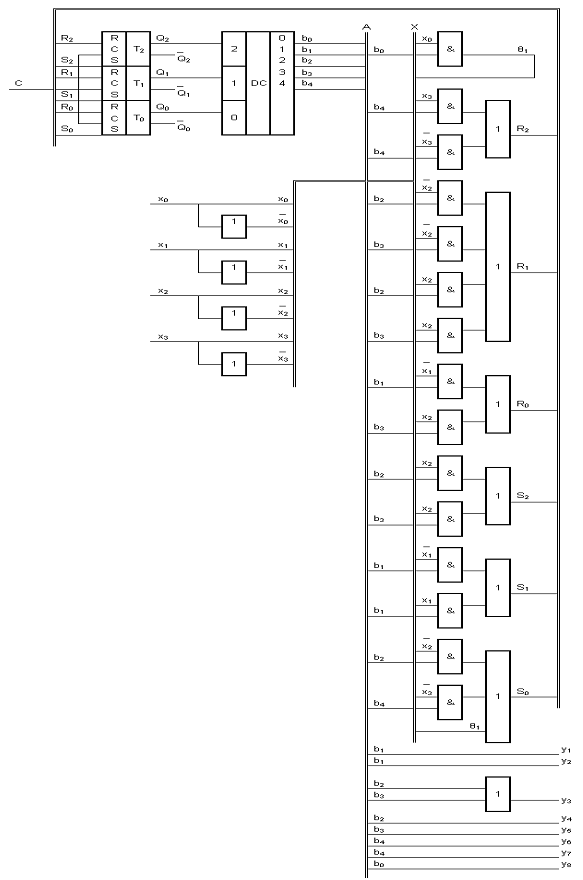
Легко заметить, что использование узлов в ГСА автомата Мура позволило значительно упростить функции выходов и переходов. 6) Построение ФСА автомата Мура.

Рис.4. ФСА автомата Мура на жёсткой логике.

Ссылки

• Участник:Logic-samara