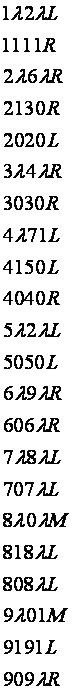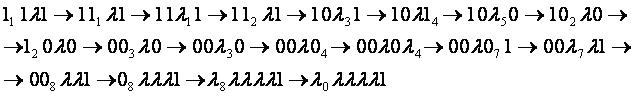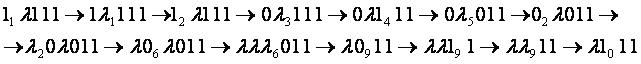Машина Тьюринга

Машина Тьюринга (МТ) — это абстрактная вычислительная машина для выполнения программ, предложенная английским математиком Аланом Мэтисоном Тьюрингом в 1936 году.

Состав МТ

МТ состоит из управляющего устройства (каретки или считывающей и записывающей головки) и ленты, разбитой на секции (ячейки) и бесконечной в обе стороны. В каждой ячейке ленты может быть какой-либо символ конечного алфавита, включающего пробел. За один шаг каретка может считать и записать символ алфавита в том месте, где она стоит и сдвинуться на одну позицию влево или вправо или остаться на месте. Управляющее устройство может находиться в одном из множества состояний. Число возможных состояний управляющего устройства конечно и точно задано. Управляющее устройство работает согласно правилам перехода (командным строкам), которые представляют алгоритм (программу). Конкретная программа для МТ задаётся перечислением элементов множества букв алфавита, множества состояний и набором правил, по которым работает МТ. Для каждой возможной конфигурации имеется ровно одно правило. Правил нет только для заключительного состояния, попав в которое машина останавливается. Работа МТ определяется программой, состоящей из конечного числа командных строк.

Виды команд:

• сдвиг вправо
• сдвиг влево
• остаться на месте
• запись символа алфавита в ячейку
• перейти в состояние из множества

Введём обозначения:

n — число состояний управляющего устройства без конечного;

Q={q₀, q₁, q₂, …, q_n} — множество состояний управляющего устройства с конечным состоянием (q₀);

k — число символов алфавита;

A={a₁, a₂, …, a_k} — алфавит с пробелом (λ);

s₁ — номер состояния, в котором управляющее устройство находится до выполнения команды;

s₂ — номер состояния, в которое управляющее устройство переходит после выполнения команды;

a₁ — считываемый символ a₁;

a₂ — записываемый символ a₂;

R — сдвиг вправо;

L — сдвиг влево;

M — оставание на месте.

Виды командных строк:

s₁a₁s₂a₂M — при считывании символа a₁ в состоянии s₁ записать символ a₂, перейти в состояние s₂ и остаться на месте;

s₁a₁s₂a₂R — при считывании символа a₁ в состоянии s₁ записать символ a₂, перейти в состояние s₂ и осуществить сдвиг каретки вправо на 1 ячейку;

s₁a₁s₂a₂L — при считывании символа a₁ в состоянии s₁ записать символ a₂, перейти в состояние s₂ и осуществить сдвиг каретки влево на 1 ячейку.

Для работы машины Тьюринга нужно задать программу и её начальное состояние (т. е. состояние управляющей системы, состояние ленты и позицию каретки). Предполагается, что неопределённая часть ленты заполнена символами пробела, т.е. она чистая.

После запуска программы на МТ возможны следующие варианты:

• работа может закончиться если система переходит в терминальное (конечное) состояние;
• работа никогда не закончится (т.е.программа составлена не корректно).

Пример задачи

, где x, y - неотрицательные целые числа.

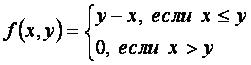
Программа для МТ

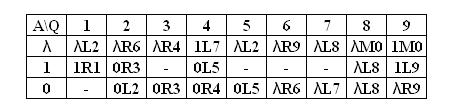
Таблица для программы

Примеры работы МТ:

Введём обозначения:

1 — число 0;

11 — число 1;

111 — число 2;

1^x+1 — неотрицательное целое число x;

1^y+1 — неотрицательное целое число y;

1^x+1λ1^y+1 — набор значений аргументов (x,y).

Пример 1

Входные данные: 1₁1λ1.

Выходные данные: λ₀λλλλ1.

Пример 2

Входные данные: 1₁λ111.

Выходные данные: λ1₀11.

• Заметим, что машина Поста во многом аналогична машине Тьюринга.

Другие алгоритмы:

• алгоритм метода математической индукции;
• алгоритмы в арифметике;
• алгоритмы перевода чисел;
• комбинаторные алгоритмы;
• алгоритм сортировки;
• алгоритм определения мест;
• логистические алгоритмы;
• алгоритмы решения транспортных задач;
• алгоритмы численных методов;
• алгоритмы построенные с помощью машины Поста;
• алгоритмы построенные с помощью машины Тьюринга;
• алгоритм синтеза автомата Мили;
• алгоритм синтеза автомата Мура.

Ссылки

• Википедия. Машина Тьюринга.
• Участник:Logic-samara