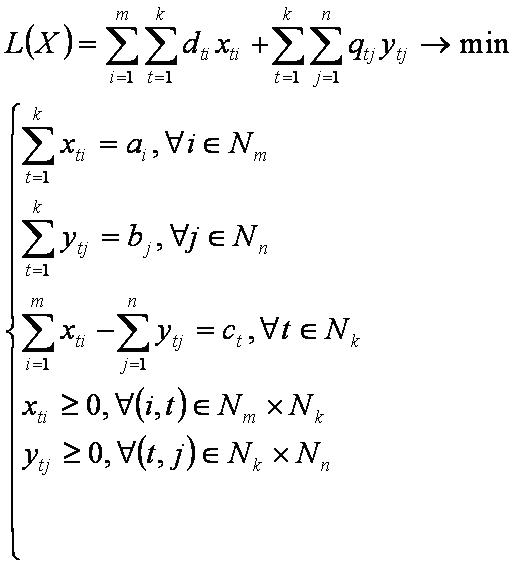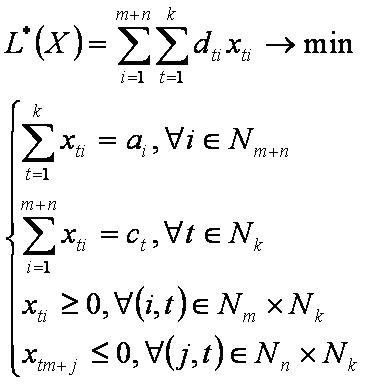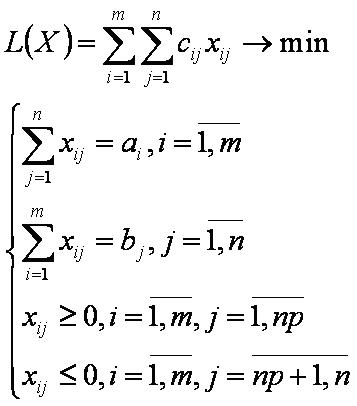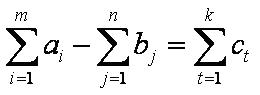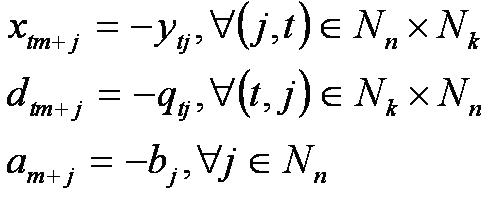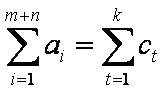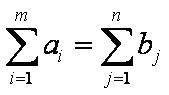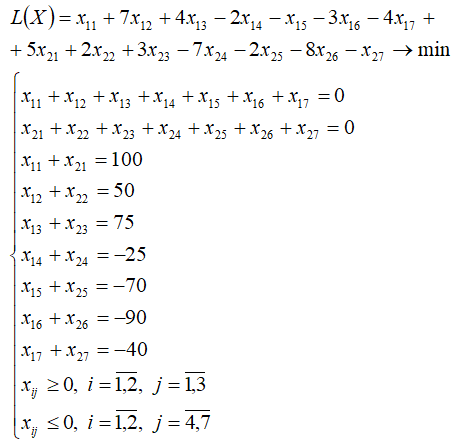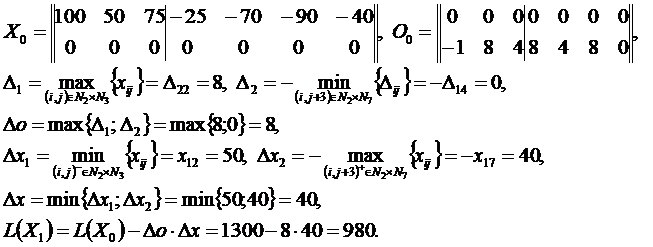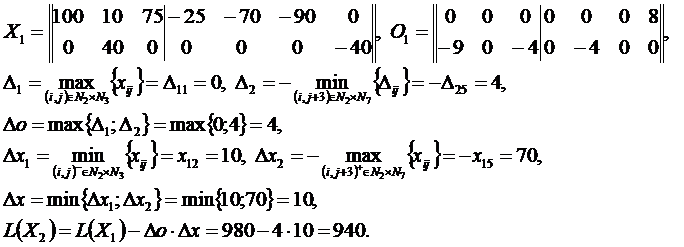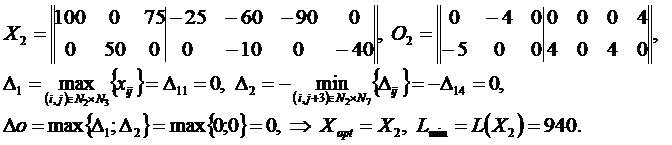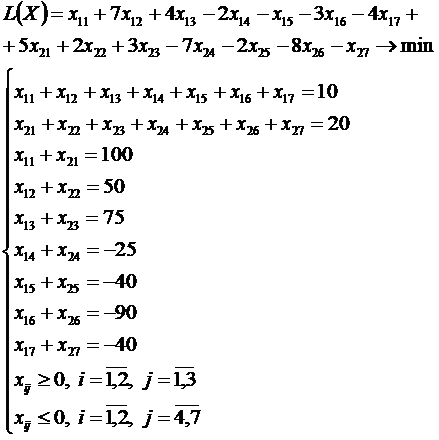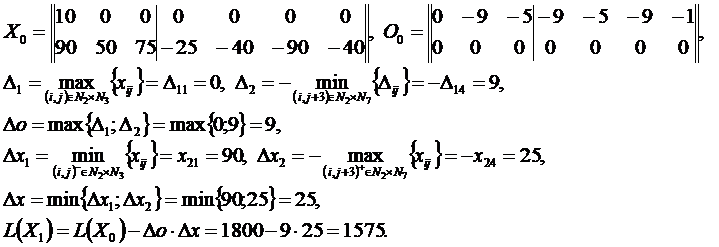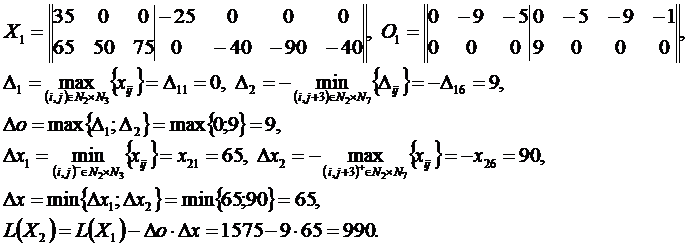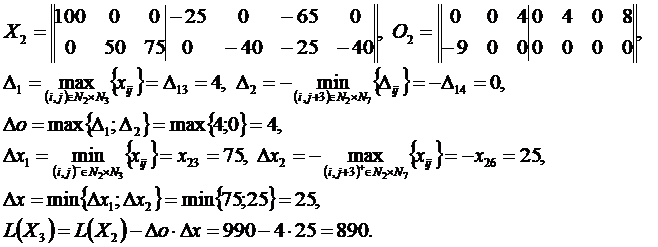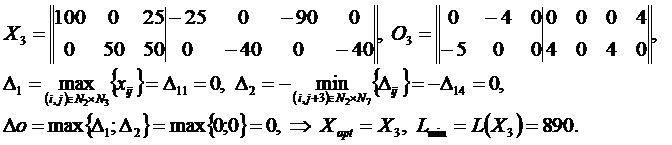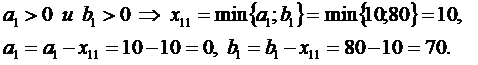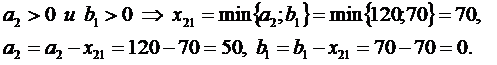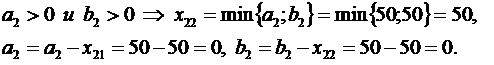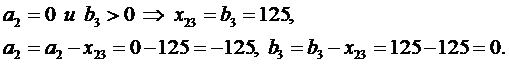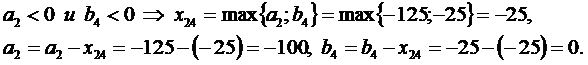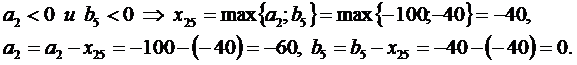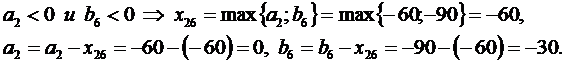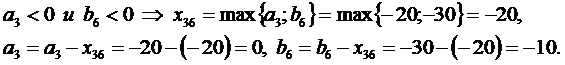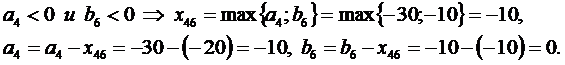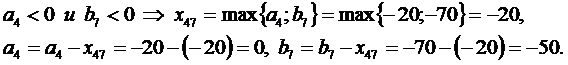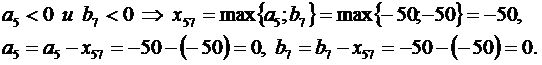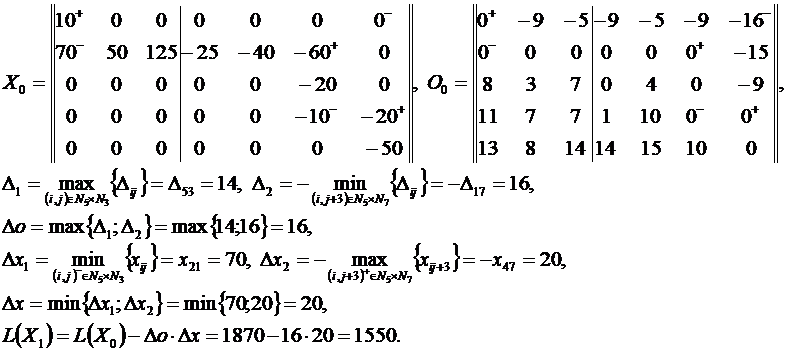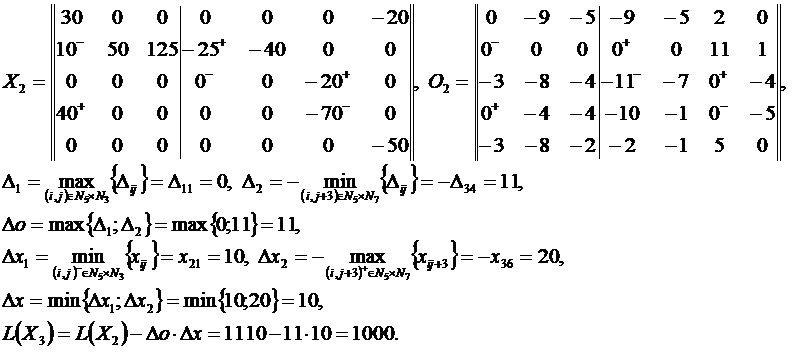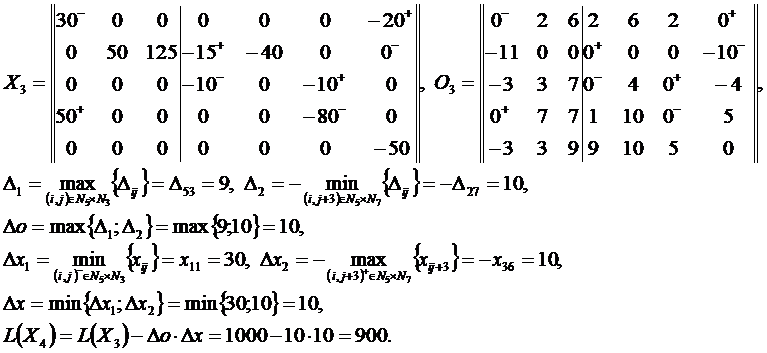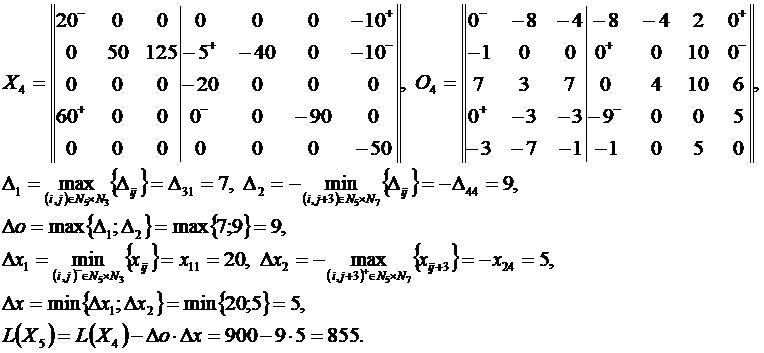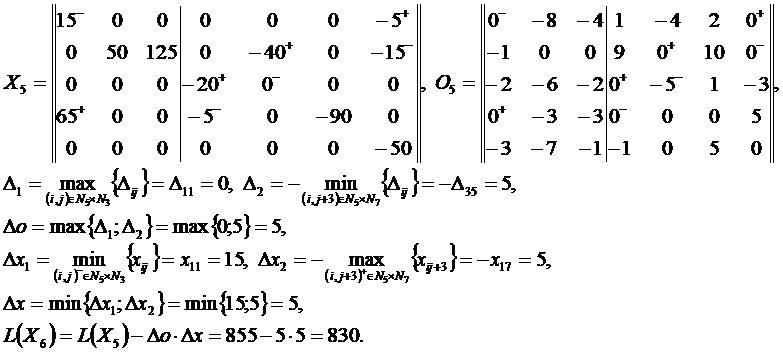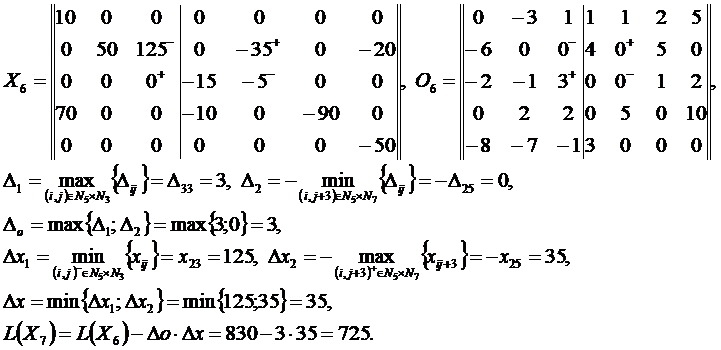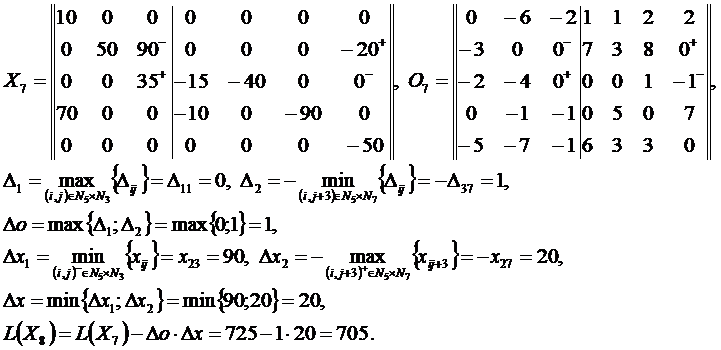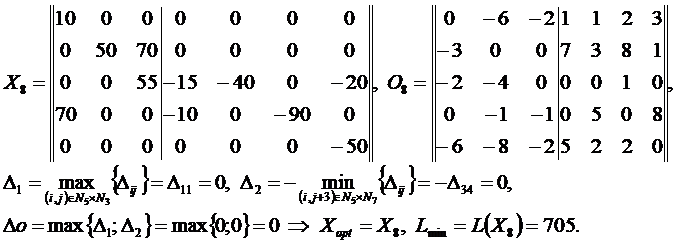Транспортная задача с промежуточными пунктами
Транспортная задача с промежуточными пунктами (ТЗПП) – это транспортная задача оптимизации перевозок с использованием промежуточных (транзитных) пунктов. ТЗПП позволяет оптимизировать мультимодальные транспортные перевозки.
Содержание
- 1 Постановка задачи ТЗПП
- 2 Условия разрешимости
- 3 Постановка эквивалентной задачи
- 4 Условия разрешимости эквивалентной задачи
- 5 Постановка классической задачи
- 6 Условия разрешимости классической задачи
- 7 Метод решения ТЗПП
- 8 Примеры ТЗПП:
- 9 Другие задачи:
- 10 Ссылки
Постановка задачи ТЗПП
Пусть имеется m поставщиков (A1,A2,…,Am), n потребителей (B1,B2,…,Bn) и k промежуточных пунктов (C1,C2,…,Ck), однородного продукта. Пусть заданы объёмы поставок ai продукта поставщиком Ai, объёмы потребностей bj в продукте у потребителя Bj, объёмы дополнительных потребностей ct в продукте в промежуточном пункте (на складе) Ct, причём если ct<0, то дополнительные потребности являются избытком. Пусть известны транспортные расходы dti на перевозку единицы продукта от поставщика Ai на склад Ct, и транспортные расходы qtj на перевозку единицы продукта со склада Ct к потребителю Bj и необходимо определить план перевозок с минимальной суммой транспортных расходов, тогда транспортная задача с промежуточными пунктами формулируется следующим образом:
где xti — объём перевозок продукта от поставщика Ai на склад Ct,
ytj — объём перевозок продукта со склада Ct к потребителю Bj.
Условия разрешимости
Для разрешимости задачи необходимо выполнение условий баланса:
то есть необходимо, чтобы объём поставок продукта поставщиками минус объём потребностей в нём у потребителей равнялся объёму дополнительных потребностей продукта на складе. В этом случае транспортная задача с промежуточными пунктами называется закрытой.
Постановка эквивалентной задачи
Введём новые обозначения:
Математическая модель эквивалентной задачи принимает следующий вид:
Условия разрешимости эквивалентной задачи
Для разрешимости эквивалентной задачи необходимо выполнение условий баланса:
то есть необходимо, чтобы объём поставок продукта на склады и объём отрицательных поставок со складов (потребностей в продукте) равнялся объёму дополнительных потребностей в продукте на складах. В этом случае транспортная задача с промежуточными пунктами называется закрытой.
Постановка классической задачи
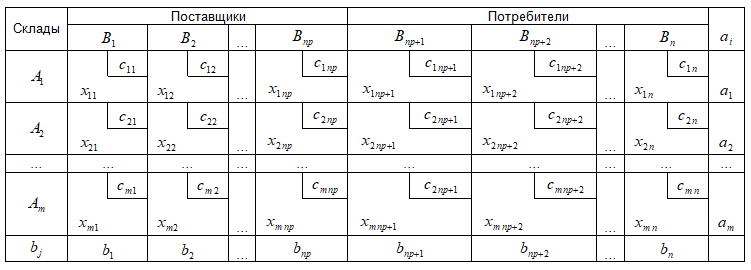
В экономической транспортной системе имеются n конечных пунктов (np поставщиков продукции и n-np потребителей продукции) и m промежуточных пунктов (складов). Продукция перевозится от поставщиков на склады, будем обозначать эти перевозки положительными переменными xij≥0, (i=1,m,j=1,np). А со складов часть продукции перевозится потребителям - их обозначим отрицательными переменными xij≤0, (i=1,m,j=np+1,n). Объёмы поставок поставщиков обозначим положительными числами bj>0, (j=1,np), объёмы потребностей потребителей обозначим отрицательными числами bj<0, (j=np+1,n). Для упрощения метода решения задачи, будем считать, что склады имеющие дополнительные (внутренние) потребности продукции расположены вначале (в любом порядке) списка, а склады имеющие излишки продукции или нулевые остатки – в конце (в любом порядке). Если склад имеет дополнительные потребности продукции, то обозначим их положительными числами ai>0, (i=1,mp). Если склад имеет излишки продукции или нулевые остатки, то обозначим их числами ai≤0, (i=mp+1,m). Транспортные тарифы на перевозку единицы продукции от поставщика на склад выразим положительными числами cij>0, (i=1,m,j=1,np), транспортные тарифы на перевозку со склада к потребителю выразим отрицательными числами cij<0, (i=1,m,j=np+1,n). Тогда математическая модель задачи принимает вид:
Классическая транспортная задача с промежуточными пунктами может быть представлена в виде таблицы
Условия разрешимости классической задачи
Для разрешимости классической задачи необходимо выполнение условий баланса:
то есть необходимо, чтобы алгебраическая сумма объёмов продукта промежуточных пунктов равнялась алгебраической сумме объёмов продукта конечных пунктов. В этом случае транспортная задача с промежуточными пунктами называется закрытой.
Метод решения ТЗПП
Необходимо найти начальное опорное решение, например, методом северо-западного угла для ТЗПП.
Затем транспортная задача с промежуточными пунктами решается обобщённым методом потенциалов для решения ТЗ, модифицированным с учётом отрицательных перевозок.
Метод северо-западного угла
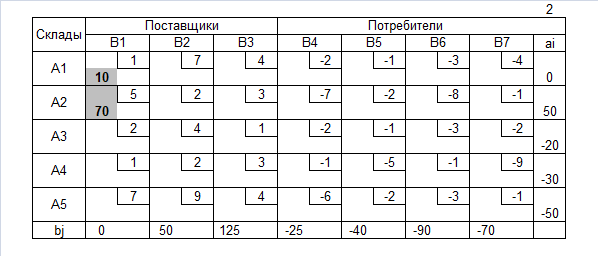
Метод северо-западного угла для нахождения допустимого решения транспортной задачи с промежуточными пунктами аналогичен одноимённому методу для транспортной задачи и состоит в последовательном назначении перевозок для клеток транспортной таблицы, находящихся в верхних (северных) строках и в левых (западных) столбцах. Процесс заполнения клеток (распределения перевозок) для ТЗПП осуществляется в три этапа и продолжается до тех пор пока у поставщиков имеются нераспределённые положительные остатки или у потребителей имеются неудовлетворённые отрицательные потребности.
1.Сначала удовлетворяем дополнительные потребности складов (ai>0) за счёт поставщиков (bj>0), т.е. назначаем соответствующие положительные перевозки по формулам: xij=min(ai,bj), ai=ai-xij, bj=bj-xij.
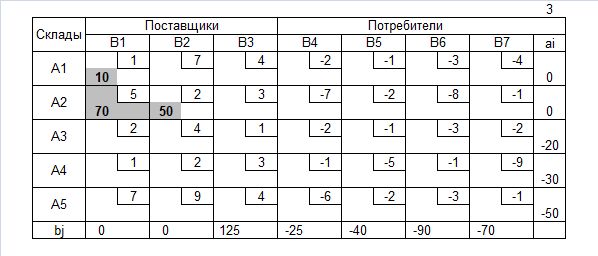
2.Затем распределяем остатки грузов от поставщиков (bj>0) на последний используемый склад, т.е. начиная с последней заполненной строки по формулам: xij=bj, ai=ai-xij, bj=0.
3.Наконец, удовлетворяем потребности потребителей (bj<0), т.е. назначаем соответствующие отрицательные перевозки по формулам: xij=max(ai,bj), aij=ai-xij, bj=bj-xij.
Метод северо-западного угла реализуется с помощью алгоритма северо-западного угла для ТЗПП.
Метод потенциалов
1.Берём решение Xmxn и базис Zmxn, найденные с помощью алгоритма северо-западного угла для ТЗПП.
2.Определяем значение целевой функции L=ΣΣcijxij и базис опорного решения Bo={(i,j)|zij=1}.
3.Определяем оценку Δo и элемент (io,jo) с помощью алгоритма расчёта потенциалов и оценок оптимальности для ТЗПП.
4.Проверяем решение на оптимальность. Если Δo=0, то решение Xmxn - оптимальное и конец работы.
5.Определяем оценку Δx, элемент (ix,jx) и новое опорное решение Xmxn с помощью алгоритма перераспределения перевозок для ТЗПП.
6.Определяем новое значение целевой функции L=L-ΔoΔx и новый базис Bo=Bo\(ix,jx)U(io,jo). Переходим к пункту 3.
Примеры ТЗПП:
Пример 1
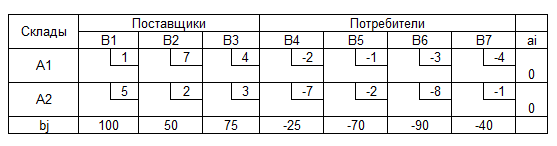
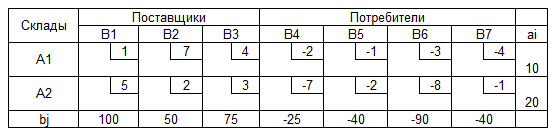
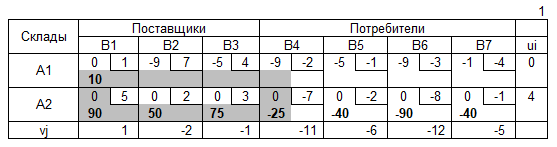
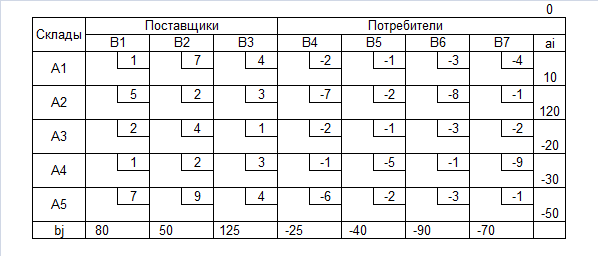
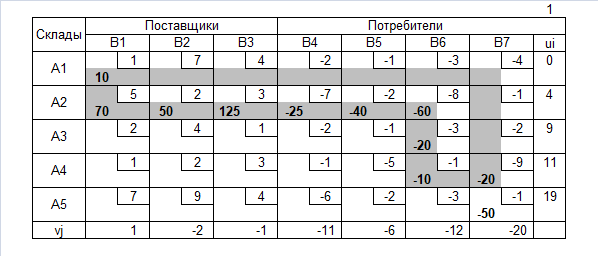
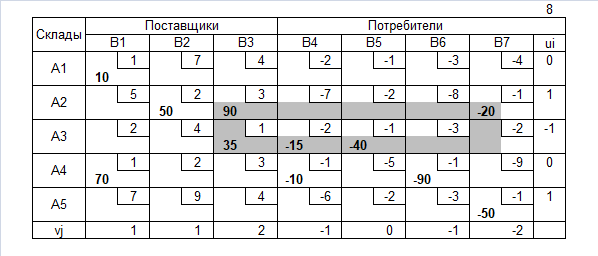
Транспортная таблица
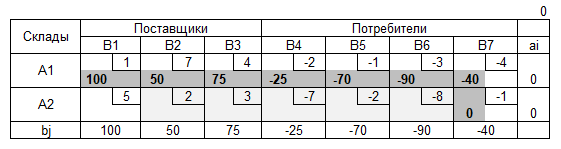
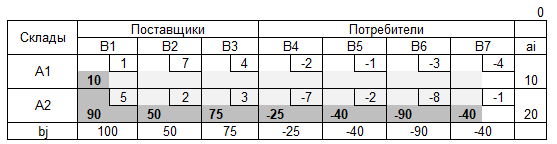
Допустимое решение
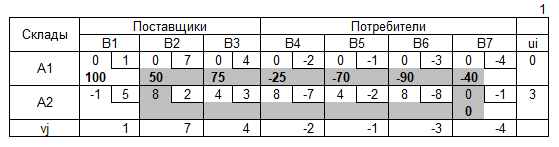
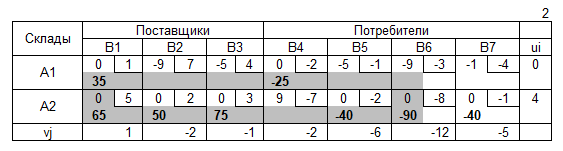
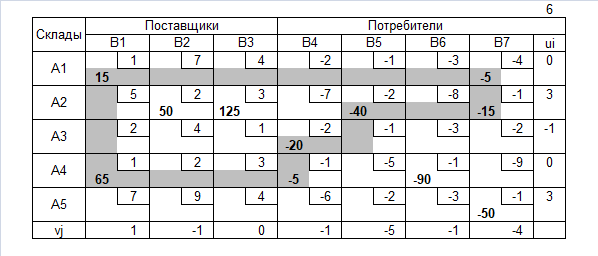
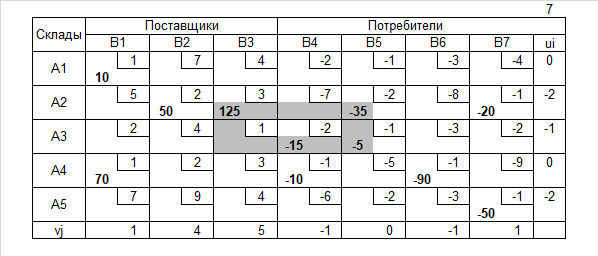
Решение методом потенциалов
Пример 2
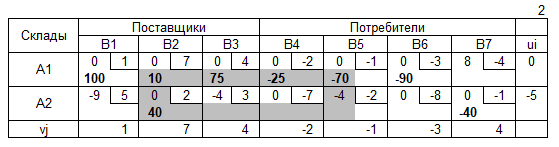
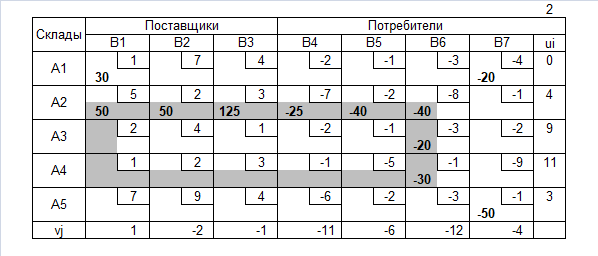
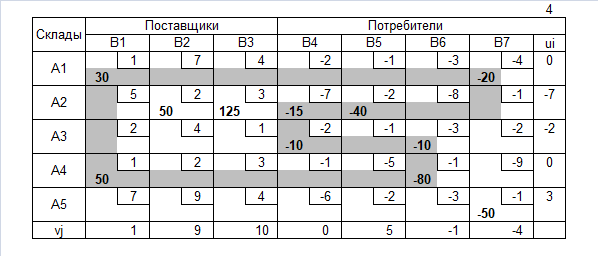
Транспортная таблица
Допустимое решение
Решение методом потенциалов
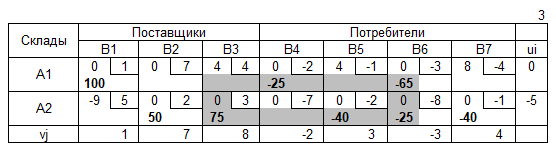
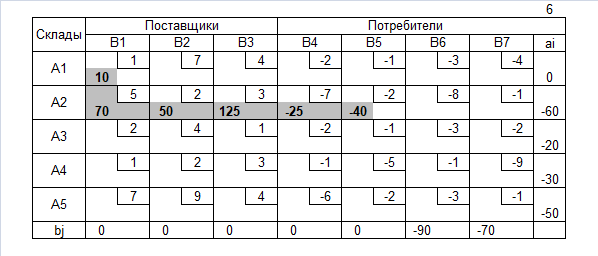
Пример 3
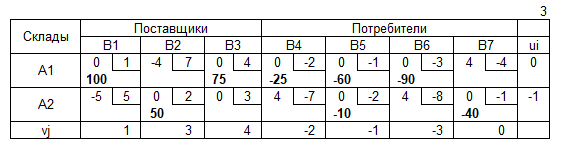
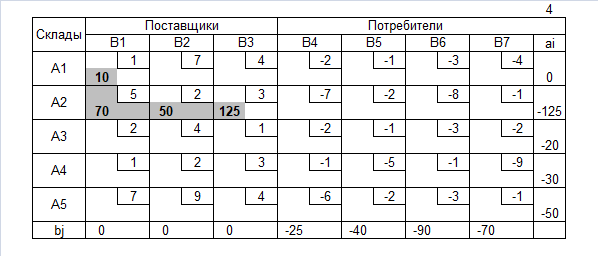
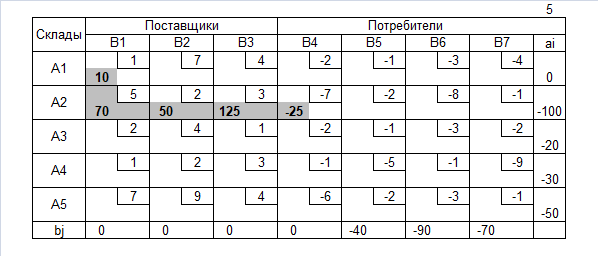
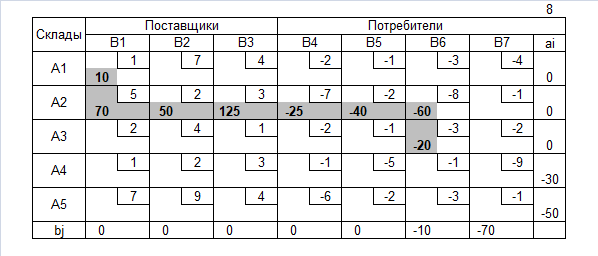
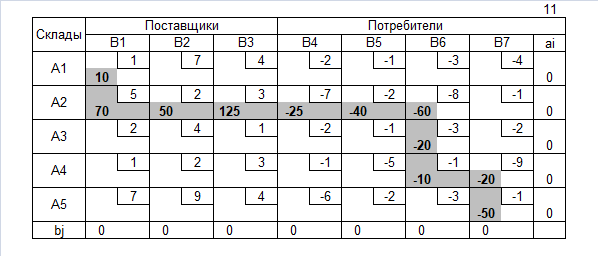
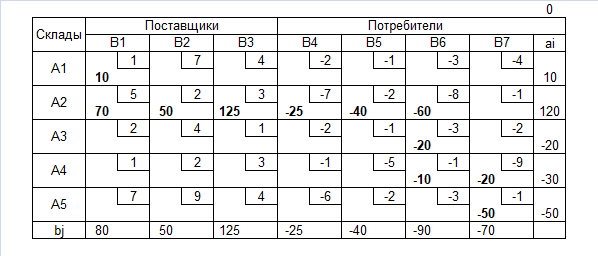
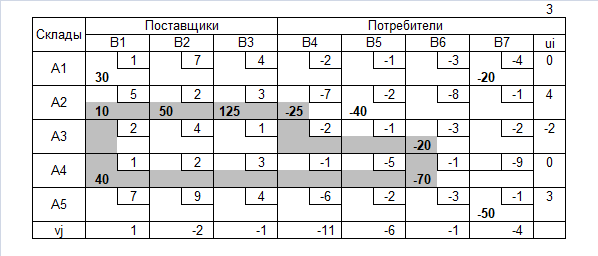
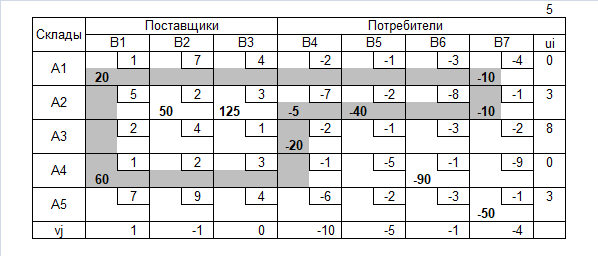
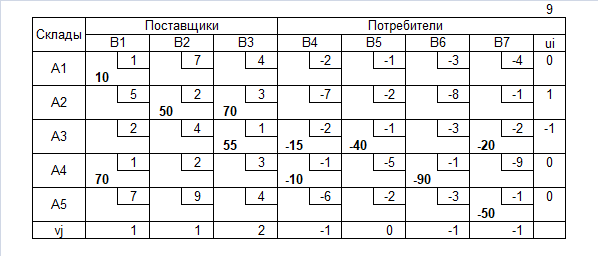
Транспортная таблица
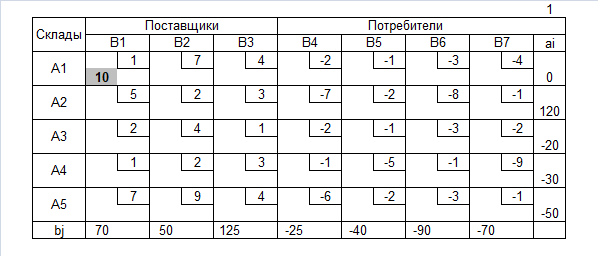
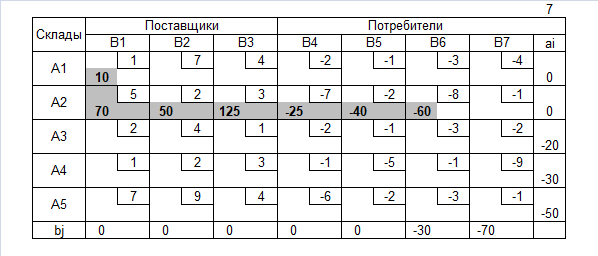
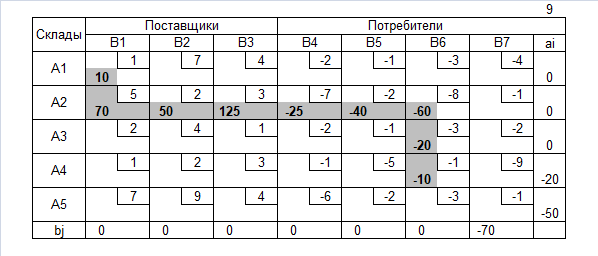
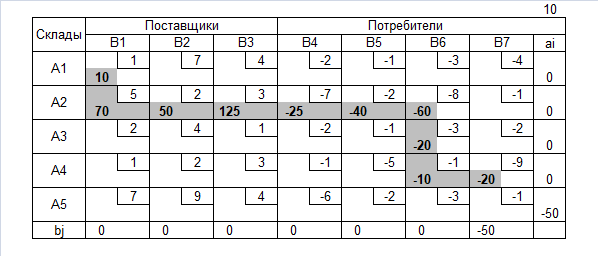
Нахождение допустимого решения
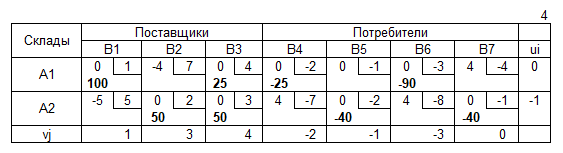
Допустимое решение
Решение методом потенциалов
Другие задачи:
- Транспортная задача;
- Распределительная задача;
- Задача о назначениях;
- Транспортная задача с промежуточными пунктами;
- Транспортная задача с промежуточными пунктами с запретами;
- Транспортная задача с промежуточными пунктами и ограничением по транзиту;
- Открытая транспортная задача с промежуточными пунктами;
- Открытая транспортная задача с промежуточными пунктами 1;
- Открытая транспортная задача с промежуточными пунктами 2;
- Открытая транспортная задача с промежуточными пунктами 3;
- Открытая транспортная задача с промежуточными пунктами 4;
- Трёхиндексная транспортная задача;
- Трёхиндексная транспортная задача с аксиальными суммами;
- Трёхиндексная транспортная задача с промежуточными пунктами.
Ссылки
- Krivopalov V. Y., Krivopalov Y. A. The potential method for solving the transportation problem with transit points. New Magenta Papers. Magenta Technology, 2013. — Vol.2 — P.31-38.
- Кривопалов В. Ю., Метод северо-западного угла для нахождения допустимого решения транспортной задачи с промежуточными пунктами. Сборник конференции ПИТ-2014, СГАУ, стр.369-372. http://www.ssau.ru/files/events/2014/pit_14_1_6.pdf
- Кривопалов В. Ю., Обобщённый метод потенциалов для решения транспортной задачи с промежуточными пунктами. Сборник Х конференции «Наука. Творчество» 2014, Самара-Москва, Т.1,стр.23-29.
- Участник:Logic-samara