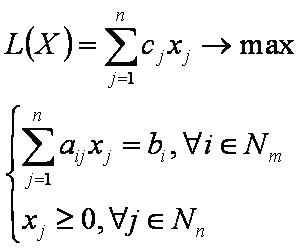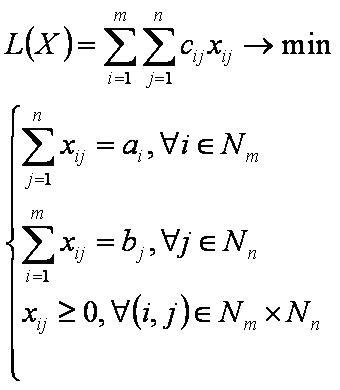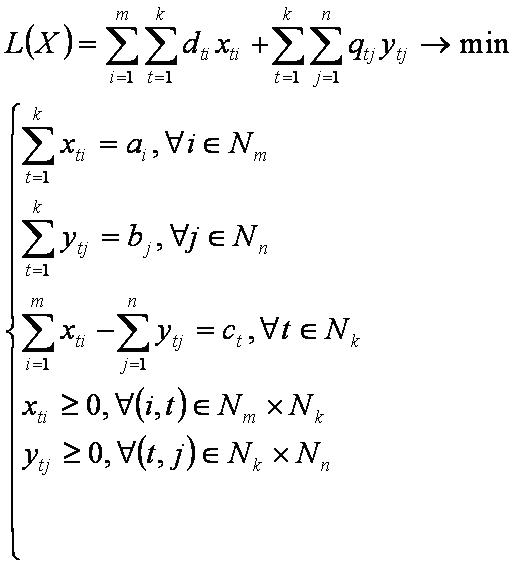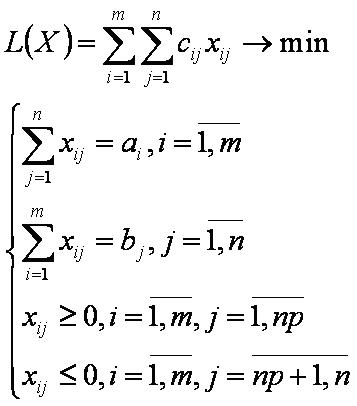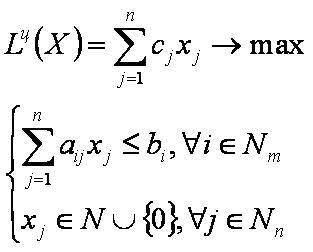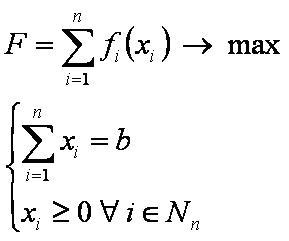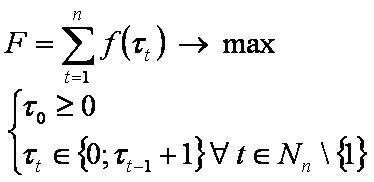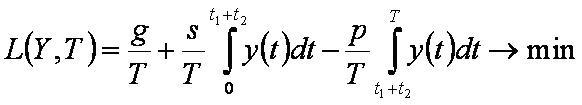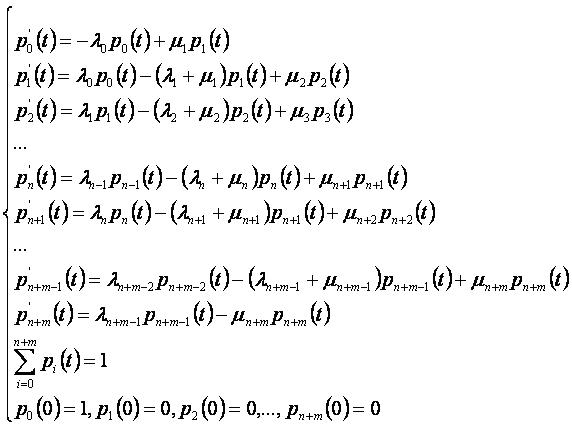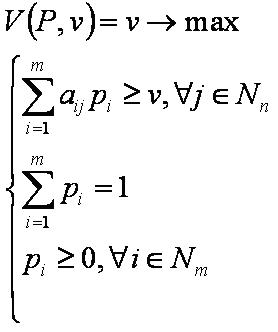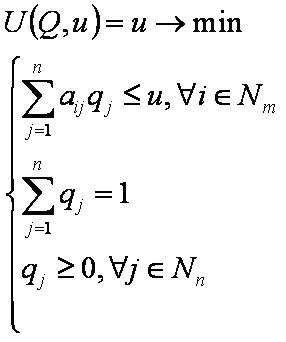Математическая модель

Mатематическая модель — это формула, уравнение, неравенство или их система, описывающие задачу, объект или процесс.

Математические модели

Задачи линейного программирования:

Каноническая задача

Транспортная задача

Другие задачи:

• Производственная задача (ПЗ);
• Общая прямая задача (ОПЗ);
• Общая двойственная задача (ОДЗ);
• Задача о назначениях (ЗН);
• Распределительная задача (РЗ);
• Трёхиндексная транспортная задача (ТТЗ).

Транспортные задачи с промежуточными пунктами:

Транспортная задача с промежуточными пунктами

Классическая транспортная задача с промежуточными пунктами

Другие задачи:

• Транспортная задача с промежуточными пунктами с запретами;
• Транспортная задача с промежуточными пунктами и ограничением по транзиту;
• Открытая транспортная задача с промежуточными пунктами 1;
• Открытая транспортная задача с промежуточными пунктами 2;
• Открытая транспортная задача с промежуточными пунктами 3;
• Открытая транспортная задача с промежуточными пунктами 4.

Задачи целочисленного программирования:

Задача целочисленного программирования

Другие задачи:

• Задача о рюкзаке;
• Задача о рюкзаке без повторений;
• Задача о рюкзаке с ограниченным числом повторений.

Задачи динамического программирования:

Задача распределения средств

Задача замены оборудования

Системы управления запасами:

Система управления запасами

Примеры систем:

• СУЗ с постоянным спросом;
• СУЗ с естественной убылью.

Системы массового обслуживания:

Система массового обслуживания

Примеры систем:

• СМО с отказами;
• СМО с очередью;
• СМО с ограниченным временем ожидания;
• СМО замкнутая без очереди;
• СМО замкнутая с очередью;
• СМО с очередью и с взаимопомощью;
• СМО с отказами и с взаимопомощью;
• СМО с бесконечным числом каналов;
• СМО с бесконечной очередью.

Матричные игры:

Задача первого игрока

Задача второго игрока

Примеры моделей:

• Модели ЛП;
• Модели ТЗПП;
• Модели ЦП;
• Модели ДП;
• Модели СУЗ;
• Модели СМО;
• Модели Игр.

Ссылки

• Юдин Д. Б., Гольштейн Е. Г. Линейное программирование., М.,1963.
• Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа, М.,1969.
• Овчаров Л. А. Прикладные задачи теории массового обслуживания, «Машиностроение», М.,1969.
• Рыжиков Ю. И. Управление запасами, «Наука», М.,1969.
• Корбут А. А., Финкельштейн Ю. Ю. Дискретное программирование, «Наука», М.,1969.
• Емеличев В. А., Ковалев М. М., Кравцов М. К., Многогранники. Графы. Оптимизация. — М.,1981, стр.313.
• Справочник по математике для экономистов. Под ред. проф. В.И.Ермакова. М.:«Высшая школа», 1987.
• Krivopalov V. Y., Krivopalov Y. A. The potential method for solving the transportation problem with transit points. New Magenta Papers. Magenta Technology, 2013. — Vol.2 — P.31-38.
• Кривопалов В. Ю., Обобщённый метод потенциалов для решения транспортной задачи с промежуточными пунктами. Сборник Х конференции «Наука. Творчество» 2014, Самара-Москва, Т.1,стр.23-29.
• Участник:Logic-samara