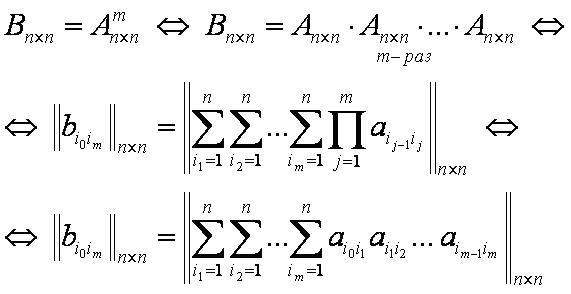Возведение в степень матрицы

Возведение в степень матрицы – это операция умножения матрицы на саму себя фиксированное число (степень) раз. Число матриц-сомножителей равно степени.

Обозначения

Введём обозначения:

n – число строк и столбцов матрицы;

m – степень матрицы, натуральное число;

nxn – размерность матриц;

a_ij – элемент матрицы A, лежащий на пересечении i-ой строки и j-ого столбца матрицы;

b_ij – элемент матрицы B, лежащий на пересечении i-ой строки и j-ого столбца матрицы;

– матрица A – матрица-сомножитель;

– матрица B – матрица-произведение.

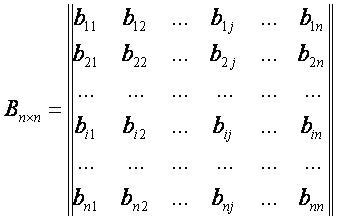
Формула

• Заметим, что возводить в степень можно только квадратные матрицы.
• Возведение в степень единичной матрицы (E) даёт единичную E^k = E.

Другие операции:

• сложение матриц;
• вычитание матриц;
• умножение матрицы на число;
• умножение матриц;
• умножение элементов матриц;
• деление элементов матриц;
• возведение в квадрат элементов матрицы;
• извлечение корня из элементов матрицы;
• деление матриц;
• транспонирование матрицы;
• обращение матрицы;
• обращение клеточной матрицы;
• возведение в степень матрицы;
• нахождение определителя;
• нахождение минора;
• нахождение алгебраического дополнения.

Ссылки

• Участник:Logic-samara