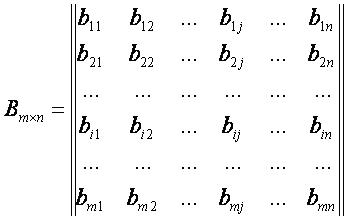Деление матриц
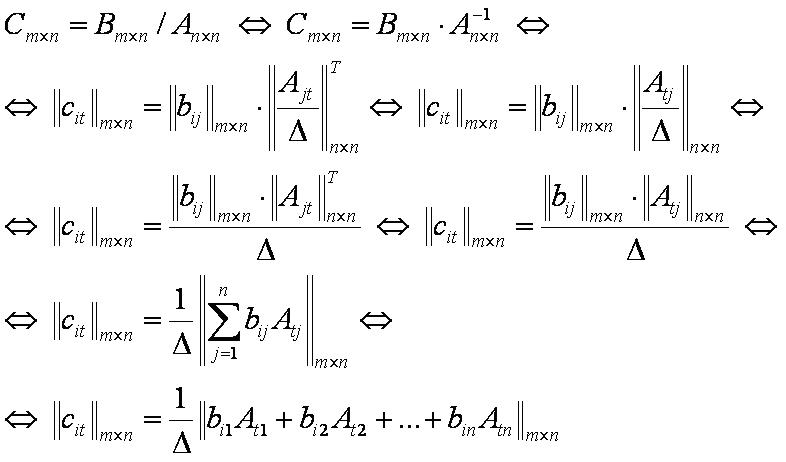
Частное от деления двух матриц – это матрица с элементами, равными сумме произведений соответствующих элементов строк матрицы-делимого и элементов столбцов обратной матрицы-делителя.
Обозначения
m – число строк матрицы-делимого и матрицы-частного;
n – число строк матрицы-делителя и число столбцов для всех матриц;
mxn – размерность матрицы-делимого и матрицы-частного;
nxn – размерность матрицы-делителя;
aij – элемент матрицы A, лежащий на пересечении i-ой строки и j-ого столбца матрицы;
bij – элемент матрицы B, лежащий на пересечении i-ой строки и j-ого столбца матрицы;
cij – элемент матрицы C, лежащий на пересечении i-ой строки и j-ого столбца матрицы;
Aij – aлгебраическое дополнение к элементу aij матрицы A;
Δ – определитель матрицы A;
Формула
- Заметим, что делить можно только матрицы у которых число столбцов матрицы-делимого совпадает с числом столбцов матрицы-делителя, причём матрица-делитель квадратная матрица с определителем отличным от нуля.
Другие операции:
- сложение матриц;
- вычитание матриц;
- умножение матрицы на число;
- умножение матриц;
- умножение элементов матриц;
- деление элементов матриц;
- возведение в квадрат элементов матрицы;
- извлечение корня из элементов матрицы;
- деление матриц;
- транспонирование матрицы;
- обращение матрицы;
- обращение клеточной матрицы;
- возведение в степень матрицы;
- нахождение определителя;
- нахождение минора;
- нахождение алгебраического дополнения.