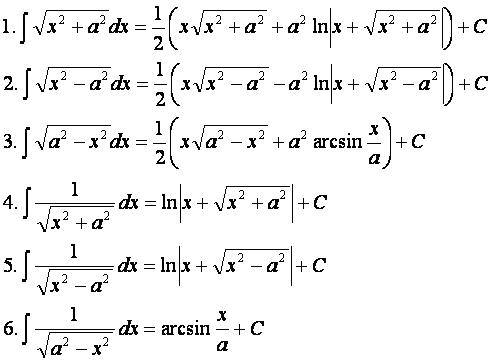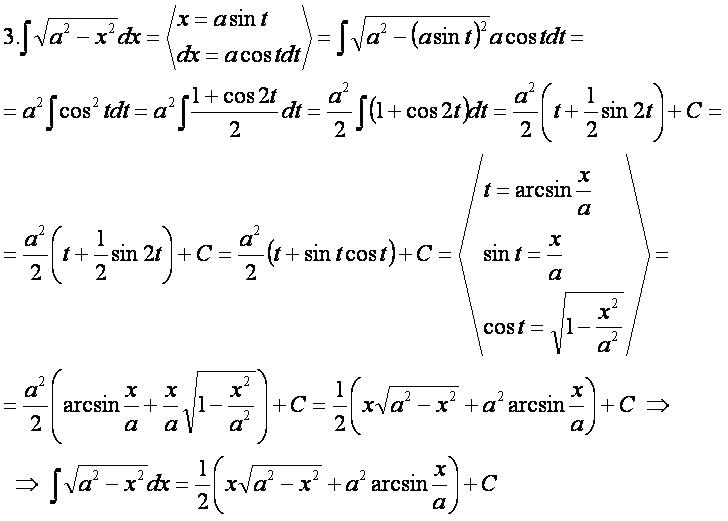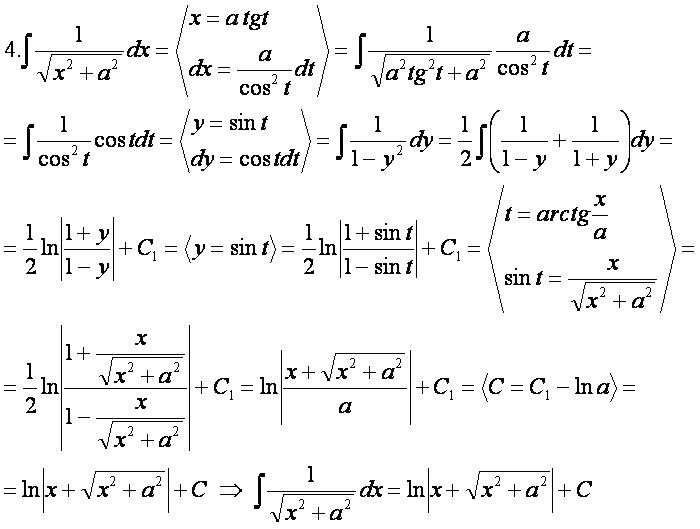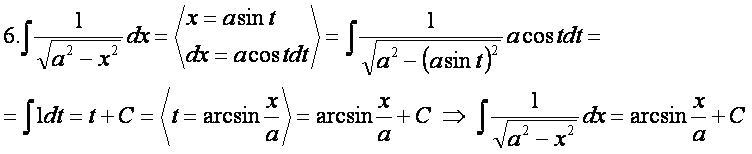Интегралы функций с корнями — различия между версиями
(начало) |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 14: | Строка 14: | ||
[[файл:ИНТ316.JPG]] | [[файл:ИНТ316.JPG]] | ||
| − | == [[ | + | == [[Математический анализ|Другие интегралы:]] == |
{{Список Инт}} | {{Список Инт}} | ||
== Ссылки == | == Ссылки == | ||
| − | + | [[Категория:Математика]][[Категория:Функции]] | |
| − | [[Категория: | ||
Текущая версия на 14:41, 18 февраля 2025
Интегралы функций с корнями — это интегралы с подынтегральными функциями, содержащими знак корня (радикала).
Содержание
Примеры
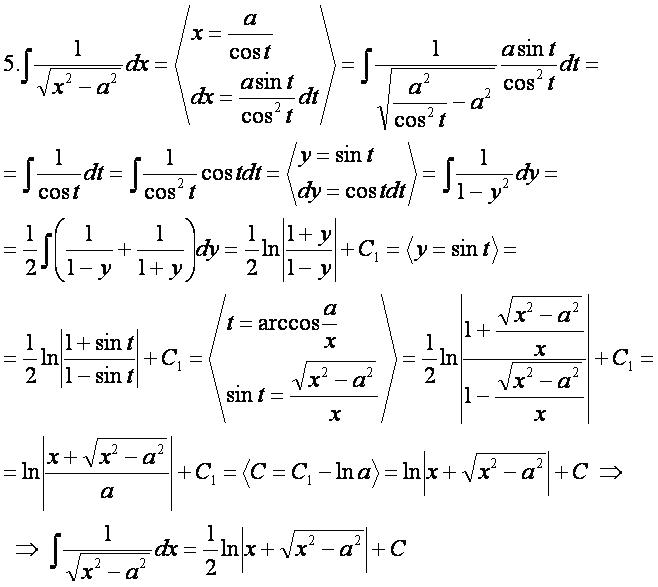
Вывод формул:
Другие интегралы:
- интеграл;
- интегралы элементарных функций;
- интегралы дробно-рациональных функций;
- интегралы функций с корнями;
- интегралы тригонометрических функций;
- интегралы обратных тригонометрических функций;
- интегралы гиперболических функций;
- интегралы обратных гиперболических функций;
- интеграл Фурье;
- интеграл Фурье комплексный;
- эллиптические интегралы;
- интегралы, определяемые методом замены переменных;
- интегралы, определяемые по интегральным равенствам;
- интегралы, определяемые по интегральным формулам;
- интеграл Эйлера-Пуассона.