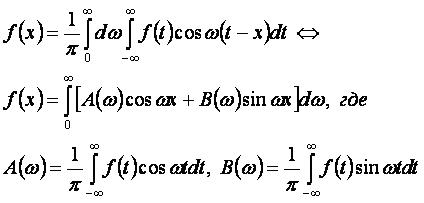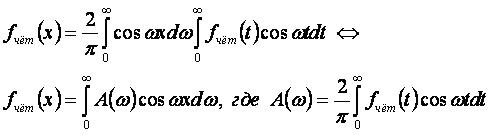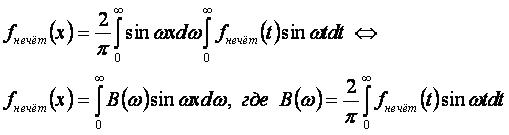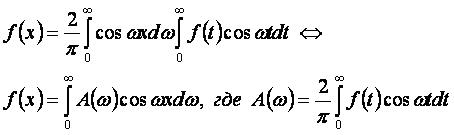Интеграл Фурье

Интеграл Фурье — это представление непериодической функции f(x) в виде интеграла, равного непрерывной сумме гармоник, зависящих от частоты ω на интервале [0,∞).

При этом говорят, что непериодическая функция f(x) имеет непрерывный спектр; частоты образующих её гармоник изменяются непрерывно. Функции A(ω) и B(ω) дают закон распределения амплитуд (и начальных фаз) в зависимости от частоты ω.

Формулы:

Представление функции f(x) на интервале (-∞,∞):

Представление чётной функции f_чёт(x) на интервале (-∞,∞):

Представление нечётной функции f_нечёт(x) на интервале (-∞,∞):

Представление функции f(x) интегралом с косинусами на интервале [0,∞):

Представление функции f(x) интегралом с синусами на интервале [0,∞):

Другие интегралы:

• интеграл;
• интегралы элементарных функций;
• интегралы дробно-рациональных функций;
• интегралы функций с корнями;
• интегралы тригонометрических функций;
• интегралы обратных тригонометрических функций;
• интегралы гиперболических функций;
• интегралы обратных гиперболических функций;
• интеграл Фурье;
• интеграл Фурье комплексный;
• эллиптические интегралы;
• интегралы, определяемые методом замены переменных;
• интегралы, определяемые по интегральным равенствам;
• интегралы, определяемые по интегральным формулам;
• интеграл Эйлера-Пуассона.

Ссылки

• Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. М.: Наука, 1973.
• Участник:Logic-samara