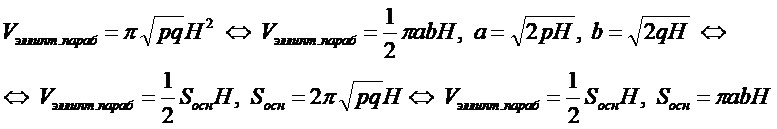Объём эллиптического параболоида

Эллиптический параболоид

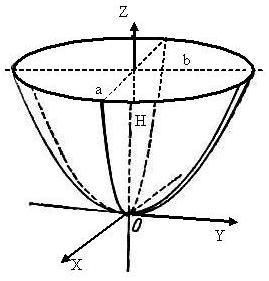
Объём эллиптического параболоида — это число, характеризующее объём, ограниченный параболоидом и плоскостью (перпендикулярной оси симметрии), в единицах измерения объёма.

Эллиптический параболоид — это поверхность, образующаяся при скольжении одной параболы по другой параболе.

Обозначения

Введём обозначения:

H — высота эллиптического параболоида;

p — фокальный параметр первой параболы;

q — фокальный параметр второй параболы;

a — первая полуось эллипса верхнего основания;

b — вторая полуось эллипса верхнего основания;

z=x²/(2p)+y²/(2q) — каноническое уравнение эллиптического параболоида;

S_осн — площадь основания (эллипс с полуосями a и b);

V_{эллипт.параб} — объём эллиптического параболоида c высотой H.

Формула

• Заметим, что при q=p формула объёма эллиптического параболоида превращается в формулу объёма параболоида вращения.

Вывод формулы

• Для вывода используется формула объём трёхмерной фигуры в прямоугольных координатах.

Другие фигуры:

• трёхмерная фигура;
• эллипсоид;
• эллиптический цилиндр;
• эллиптический конус;
• эллиптический параболоид;
• фигура вращения.

Ссылки

• Участник:Logic-samara