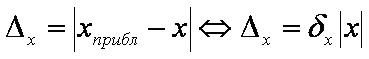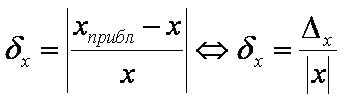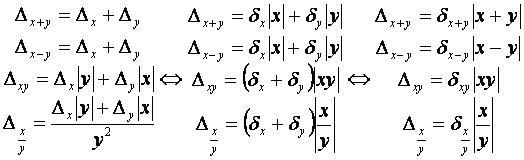Погрешность — различия между версиями
(начало) |
м |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Погрешность измерения''' — отклонение измеренного значения величины от её истинного (действительного) значения. | '''Погрешность измерения''' — отклонение измеренного значения величины от её истинного (действительного) значения. | ||
| − | + | = Погрешность = | |
Погрешность измерения является характеристикой точности измерения. | Погрешность измерения является характеристикой точности измерения. | ||
== Виды погрешности: == | == Виды погрешности: == | ||
| Строка 18: | Строка 18: | ||
[[файл:ПОГР12.JPG]] | [[файл:ПОГР12.JPG]] | ||
*Очевидно, что для формул с операцией деления знаменатель не равен нулю. | *Очевидно, что для формул с операцией деления знаменатель не равен нулю. | ||
| − | = | + | = [[Математический анализ|Другие понятия:]] = |
{{Список ДП}} | {{Список ДП}} | ||
| − | + | = Ссылки = | |
*Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970. | *Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970. | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 09:40, 19 февраля 2025
Погрешность измерения — отклонение измеренного значения величины от её истинного (действительного) значения.
Погрешность
Погрешность измерения является характеристикой точности измерения.
Виды погрешности:
- абсолютная погрешность;
- относительная погрешность.
Абсолютной погрешностью приближенного числа называется модуль разности между этим числом и его точным значением.
Относительной погрешностью приближенного числа называется отношение абсолютной погрешности приближенного числа к модулю его точного значения.
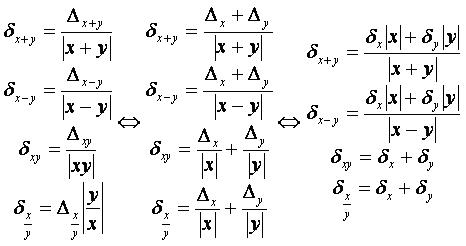
Свойства погрешности:
- Очевидно, что для формул с операцией деления знаменатель не равен нулю.
Другие понятия:
Ссылки
- Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970.