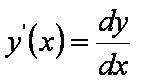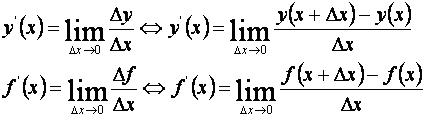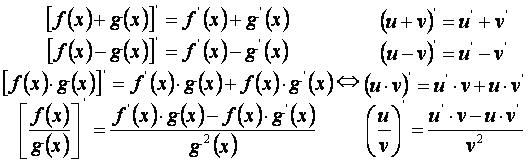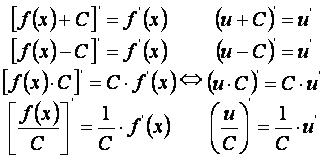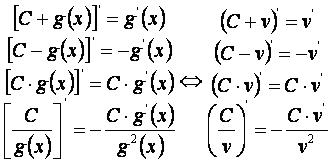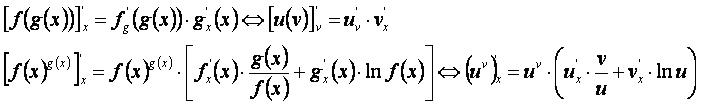Производная — различия между версиями
(начало) |
м |
||
| Строка 1: | Строка 1: | ||
'''Производная''' — это математический термин, обозначающий некую функцию, соответствующую скорости изменения функции. Нахождение производной от функции называется дифференцированием. | '''Производная''' — это математический термин, обозначающий некую функцию, соответствующую скорости изменения функции. Нахождение производной от функции называется дифференцированием. | ||
| − | + | = Производная от функции = | |
1. Определение производной через понятие [[дифференциал]]а. | 1. Определение производной через понятие [[дифференциал]]а. | ||
| Строка 34: | Строка 34: | ||
[[файл:ПРО04.JPG]] | [[файл:ПРО04.JPG]] | ||
| − | + | = [[Математический анализ|Другие понятия:]] = | |
{{Список ДП}} | {{Список ДП}} | ||
| − | + | = Ссылки = | |
*Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | *Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
[[Категория:Математика]] | [[Категория:Математика]] | ||
Версия 06:10, 7 января 2021
Производная — это математический термин, обозначающий некую функцию, соответствующую скорости изменения функции. Нахождение производной от функции называется дифференцированием.
Содержание
Производная от функции
1. Определение производной через понятие дифференциала.
Производная от функции y=f(x) равна отношению дифференциалов функции и аргумента.
2. Определение производной от функции через понятие предела.
Производная от функции y=f(x) равна пределу отношения приращения функции Δy к приращению аргумента Δx, когда приращение аргумента стремиться к нулю Δx→0.
Свойства производных
Для функций u=f(x) и v=g(x) верны правила:
При f(x) и g(x)=C получаем:
При f(x)=C и g(x) получаем:
Виды производных:
Производные элементарных функций — это производные от элементарных функций (табличные).
Производные сложных функций — это производные от функций, состоящих из внешней функции и внутренней функции (функция от функции).
Формулы производных сложных функций
Другие понятия:
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Участник:Logic-samara