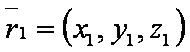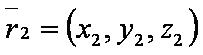Площадь поверхности параллелепипеда — различия между версиями
м |
м |
||
| Строка 6: | Строка 6: | ||
Рассмотрим параллелепипеды, в которых заданы четыре точки '''1, 2, 3, 4''', причём точки '''2, 3, 4''' являются соседними для точки '''1'''. | Рассмотрим параллелепипеды, в которых заданы четыре точки '''1, 2, 3, 4''', причём точки '''2, 3, 4''' являются соседними для точки '''1'''. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
[[файл:ВЕК71.JPG]] — радиус-вектор первой точки; | [[файл:ВЕК71.JPG]] — радиус-вектор первой точки; | ||
| Строка 30: | Строка 28: | ||
{{Список ПМГ}} | {{Список ПМГ}} | ||
== Ссылки == | == Ссылки == | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 16:21, 18 февраля 2025
Площадь поверхности параллелепипеда — это число, характеризующее параллелепипед в единицах измерения площади, равное сумме площадей его (параллелепипеда) граней.
Параллелепипед — это шестигранник с параллельными противоположными гранями (параллелограммами).
Рассмотрим параллелепипеды, в которых заданы четыре точки 1, 2, 3, 4, причём точки 2, 3, 4 являются соседними для точки 1.
Содержание
Обозначения
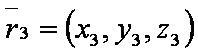
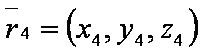
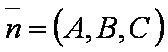
SΔ — площадь треугольника, построенного по трём заданным точкам;
Sпар — площадь поверхности параллелепипеда, построенного по четырём заданным точкам.
Формула
где