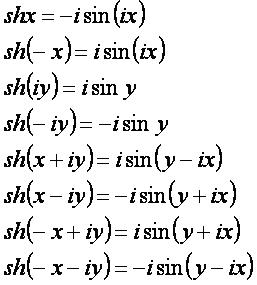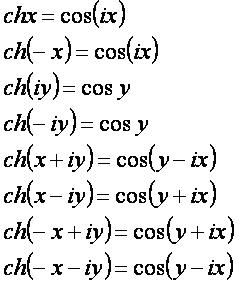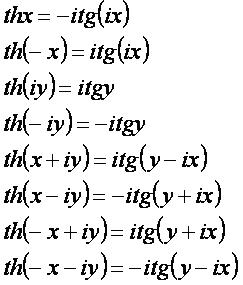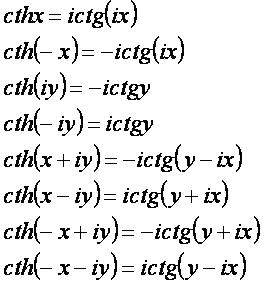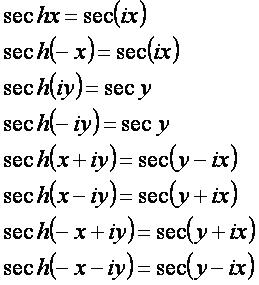Выражение гиперболических функций через тригонометрические — различия между версиями
м |
м |
||
| Строка 25: | Строка 25: | ||
== Ссылки == | == Ссылки == | ||
*Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.195. | *Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.195. | ||
| − | |||
[[Категория:Математика]][[Категория:Функции]] | [[Категория:Математика]][[Категория:Функции]] | ||
Текущая версия на 10:53, 28 декабря 2024
Выражение гиперболических функций через тригонометрические — это формулы эквивалентных преобразований для комплексных переменных.
Содержание
Обозначения
Введём обозначения:
x — действительная часть (абсцисса) переменной;
y — мнимая часть (ордината) переменной;
x+iy — комплексная переменная.
Формулы:
shx:
chx:
thx:
cthx:
sechx:
cschx:
Другие формулы:
- гиперболические функции;
- сумма гиперболических функций;
- разность гиперболических функций;
- произведение гиперболических функций;
- гиперболические функции суммы;
- гиперболические функции разности;
- гиперболические функции кратных аргументов;
- гиперболические функции двойного аргумента;
- гиперболические функции половинного аргумента;
- выражение гиперболических функций через другую;
- выражение гиперболических функций через тригонометрические;
- гиперболические функции комплексной переменной;
- производные гиперболических функций;
- дифференциалы гиперболических функций;
- интегралы гиперболических функций;
- графики гиперболических функций.
Ссылки
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.195.