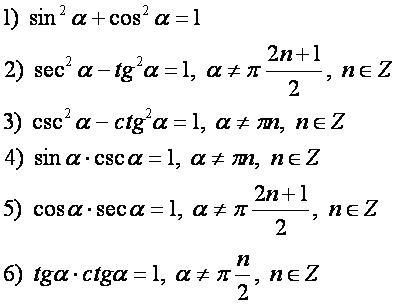Тригонометрические функции углов

Тригонометрические функции углов — это специальные функции, в которых аргументами являются углы.

Виды функций:

• синус (y=sinx);
• косинус (y=cosx);
• тангенс (y=tgx);
• котангенс (y=ctgx);
• секанс (y=secx);
• косеканс (y=cscx).

Определения:

Тригонометрические функции острого угла (0<α<π/2) определяются как отношения сторон прямоугольного треугольника.

Синусом угла (sinα) называется отношение противолежащего катета к гипотенузе.

Косинусом угла (cosα) называется отношение прилежащего катета к гипотенузе.

Тангенсом угла (tgα) называется отношение противолежащего катета к прилежащему.

Котангенсом угла (ctgα) называется отношение прилежащего катета к противолежащему.

Секансом угла (secα) называется отношение гипотенузы к прилежащему катету.

Косекансом угла (cscα) называется отношение гипотенузы к противолежащему катету.

Свойства функций:

Примеры:

Другие формулы:

• тригонометрические функции углов;
• сумма тригонометрических функций;
• разность тригонометрических функций;
• произведение тригонометрических функций;
• тригонометрические функции суммы углов;
• тригонометрические функции разности углов;
• тригонометрические формулы приведения;
• тригонометрические функции кратных углов;
• тригонометрические функции двойного угла;
• тригонометрические функции половинного угла;
• тригонометрические функции угла, полученного многократным делением пи на два;
• выражение тригонометрических функций через другую;
• выражение тригонометрических функций через гиперболические;
• тригонометрические функции комплексной переменной;
• производные тригонометрических функций;
• дифференциалы тригонометрических функций;
• интегралы тригонометрических функций;
• графики тригонометрических функций.

Ссылки

• Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.179.
• Участник:Logic-samara