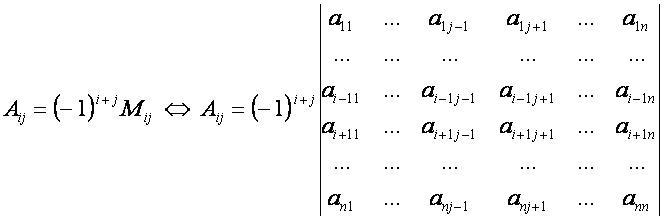Алгебраическое дополнение — различия между версиями
м |
м |
||
| Строка 11: | Строка 11: | ||
'''A<sub>ij</sub>''' – алгебраическое дополнение; | '''A<sub>ij</sub>''' – алгебраическое дополнение; | ||
| − | [[файл:МАТ10.JPG]] – матрица | + | [[файл:МАТ10.JPG]] – исходная матрица. |
== Нахождение aлгебраического дополнения == | == Нахождение aлгебраического дополнения == | ||
Для нахождения aлгебраического дополнения элемента '''a<sub>ij</sub>''' квадратной [[Матрица|матрицы]] '''n'''-го порядка необходимо сначала найти соответствующий [[минор]] '''(n-1)'''-го порядка, затем умножить его на '''(-1)<sup>i+j</sup>'''. | Для нахождения aлгебраического дополнения элемента '''a<sub>ij</sub>''' квадратной [[Матрица|матрицы]] '''n'''-го порядка необходимо сначала найти соответствующий [[минор]] '''(n-1)'''-го порядка, затем умножить его на '''(-1)<sup>i+j</sup>'''. | ||
Текущая версия на 18:06, 23 октября 2024
Алгебраическое дополнение к элементу матрицы — это суммарный коэффициент при элементе в алгебраической сумме определителя, дополняющий элемент в алгебраической сумме слагаемых определителя, содержащих этот элемент.
Обозначения
n – порядок квадратной матрицы;
nxn – размерность квадратной матрицы;
aij – элемент матрицы, лежащий на пересечении i-ой строки и j-ого столбца матрицы;
Mij – минор (n-1)-го порядка для квадратных матриц n-го порядка;
Aij – алгебраическое дополнение;
Нахождение aлгебраического дополнения
Для нахождения aлгебраического дополнения элемента aij квадратной матрицы n-го порядка необходимо сначала найти соответствующий минор (n-1)-го порядка, затем умножить его на (-1)i+j.
Другие операции:
- сложение матриц;
- вычитание матриц;
- умножение матрицы на число;
- умножение матриц;
- умножение элементов матриц;
- деление элементов матриц;
- возведение в квадрат элементов матрицы;
- извлечение корня из элементов матрицы;
- деление матриц;
- транспонирование матрицы;
- обращение матрицы;
- обращение клеточной матрицы;
- возведение в степень матрицы;
- нахождение определителя;
- нахождение минора;
- нахождение алгебраического дополнения.