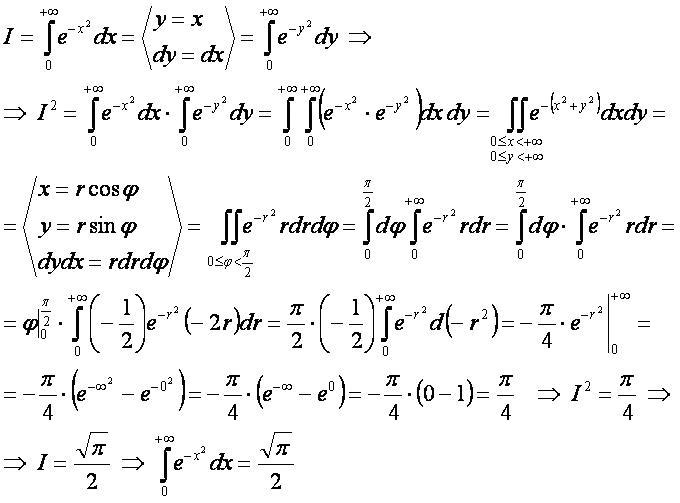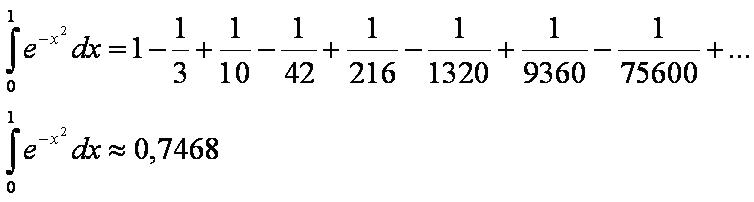Интеграл Эйлера-Пуассона — различия между версиями
(начало) |
м |
||
| Строка 1: | Строка 1: | ||
| + | = Интеграл Эйлера--Пуассона == | ||
[[файл:ИНТ601.JPG]] - '''[[интеграл]] Эйлера-Пуассона''' | [[файл:ИНТ601.JPG]] - '''[[интеграл]] Эйлера-Пуассона''' | ||
== Вывод формулы == | == Вывод формулы == | ||
| Строка 12: | Строка 13: | ||
[[файл:ИНТ605.JPG]] | [[файл:ИНТ605.JPG]] | ||
| − | + | = [[Преобразование|Другие интегралы:]] = | |
{{Список Инт}} | {{Список Инт}} | ||
| − | + | = Ссылки = | |
*Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: «Наука», 1975, стр.525. | *Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: «Наука», 1975, стр.525. | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
[[Категория:Математика]] | [[Категория:Математика]] | ||
Версия 10:32, 7 января 2021
Содержание
Интеграл Эйлера--Пуассона =

Вывод формулы
Следствие
Дополнение
Для фиксированного x имеем:
При x=1 получаем:
Другие интегралы:
- интеграл;
- интегралы элементарных функций;
- интегралы дробно-рациональных функций;
- интегралы функций с корнями;
- интегралы тригонометрических функций;
- интегралы обратных тригонометрических функций;
- интегралы гиперболических функций;
- интегралы обратных гиперболических функций;
- интеграл Фурье;
- интеграл Фурье комплексный;
- эллиптические интегралы;
- интегралы, определяемые методом замены переменных;
- интегралы, определяемые по интегральным равенствам;
- интегралы, определяемые по интегральным формулам;
- интеграл Эйлера-Пуассона.
Ссылки
- Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: «Наука», 1975, стр.525.
- Участник:Logic-samara