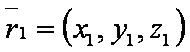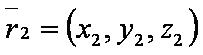Площадь поверхности параллелепипеда

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

Параллелепипед

Площадь поверхности параллелепипеда — это число, характеризующее параллелепипед в единицах измерения площади, равное сумме площадей его (параллелепипеда) граней.

Параллелепипед — это шестигранник с параллельными противоположными гранями (параллелограммами).

Рассмотрим параллелепипеды, в которых заданы четыре точки 1, 2, 3, 4, причём точки 2, 3, 4 являются соседними для точки 1.

Обозначения

Введём обозначения:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

— радиус-вектор первой точки;

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

— радиус-вектор второй точки;

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

— радиус-вектор третьей точки;

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

— радиус-вектор четвёртой точки;

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

— нормаль к плоскости, проходящей через три заданные точки;

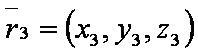
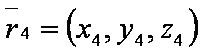
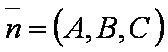
S_Δ — площадь треугольника, построенного по трём заданным точкам;

S_пар — площадь поверхности параллелепипеда, построенного по четырём заданным точкам.

Формула

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

где

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

Другие многогранники:

• призма;
• пирамида;
• усечённая пирамида;
• тетраэдр;
• параллелепипед;
• n-гранник.

Ссылки

• Участник:Logic-samara