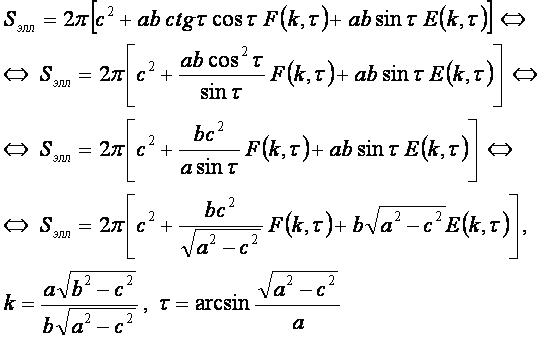Площадь эллипсоида
Площадь эллипсоида — это число, характеризующее эллипсоид в единицах измерения площади.
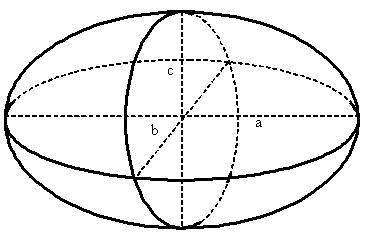
Эллипсоид (трёхосный) — это поверхность в трёхмерном пространстве, полученная деформацией сферы вдоль трёх взаимно перпендикулярных осей.
Обозначения
Введём обозначения:
a — первая (большая) полуось;
b — вторая (средняя) полуось;
c — третья (малая) полуось;
F(k,t) — эллиптический интеграл I рода;
E(k,t) — эллиптический интеграл II рода;
Sэлл — площадь поверхности эллипсоида.
Виды эллипсоида:
Эллипсоид называется трёхосным, если a>b>c.
Эллипсоид называется вытянутым вдоль оси 2a, если a>max{b,c}.
Эллипсоид называется сплюснутым вдоль оси 2c, если c<min{a,b}.
Эллипсоид называется эллипсоидом вращения вокруг оси 2a, если b=c (при a>b является вытянутым сфероидом).
Эллипсоид называется эллипсоидом вращения вокруг оси 2c, если a=b (при b>с является сплюснутым сфероидом).
Эллипсоид называется сферой, если a=b=с (является нормальным сфероидом).
Рассмотрим трёхосные эллипсоиды, для которых a>b>c.
Формула
