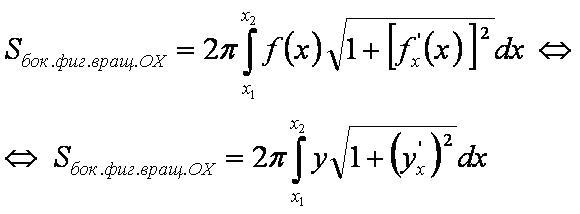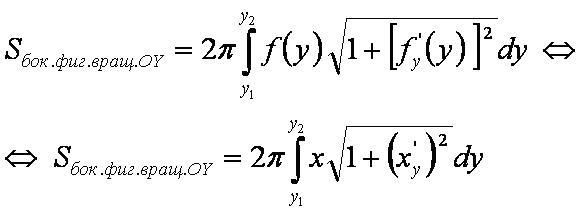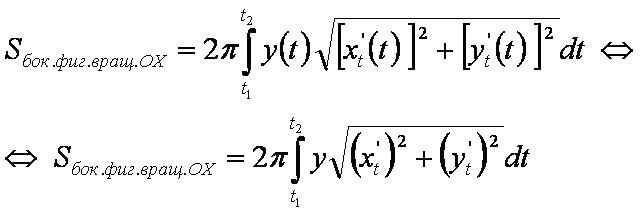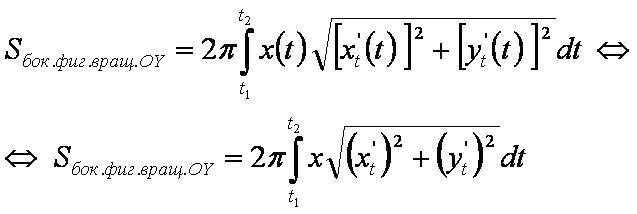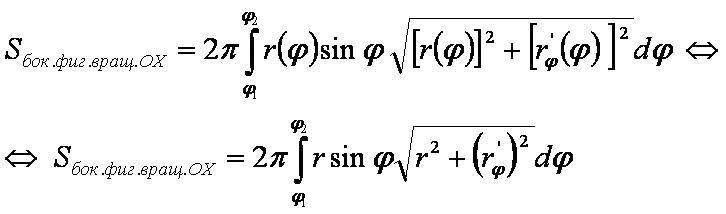Площадь поверхности фигуры вращения
Площадь поверхности фигуры вращения — это сумма площади боковой поверхности фигуры, образованной вращением образующей, и площади оснований (при наличии оснований).
Содержание
Формулы:
Формула 1
Площадь поверхности, образованной вращением кривой y=f(x) вокруг оси OX:
Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения
Формула 2
Площадь поверхности, образованной вращением кривой x=f(y) вокруг оси OY:
Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения
Формула 3
Площадь поверхности, образованной вращением кривой y=y(t) заданной параметрически вокруг оси OX:
Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения
Формула 4
Площадь поверхности, образованной вращением кривой x=x(t) заданной параметрически вокруг оси OY:
Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения
Формула 5
Площадь поверхности, образованной вращением кривой r=r(φ) в полярных координатах вокруг оси OX:
Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения
Примеры фигур:
- фигура вращения;
- шар;
- цилиндр;
- конус;
- усечённый цилиндр;
- усечённый конус;
- шаровой сегмент;
- шаровой сектор;
- шаровой слой;
- шаровой клин;
- центральный шаровой клин;
- торовый клин;
- цилиндрическая труба;
- цилиндрическое копыто;
- конусное копыто;
- шаровое копыто;
- шаровая бочка;
- круговая бочка;
- сегментное кольцо;
- тор;
- кокон;
- купол;
- сфероид;
- параболоид.
Другие формулы:
Виды формул:
- неравенства;
- операции с комплексными числами;
- операции с векторами;
- операции с матрицами;
- уравнения;
- дифференциальные уравнения;
- системы дифференциальных уравнений;
- функции;
- расстояния;
- проекции;
- точки;
- уравнения прямой;
- уравнения плоскости;
- углы;
- длины линий;
- площади фигур;
- площади поверхностей;
- объёмы.
Ссылки
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.395.
- Участник:Logic-samara
