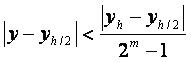Классический метод Рунге-Кутты
Классический метод Рунге-Кутты — это численный метод получения решения дифференциального уравнения.
Содержание
Описание метода
Суть метода Рунге-Кутты в пошаговом вычислении значений решения y=y(x) дифференциального уравнения вида y’=f(x,y) с начальным условием (x0,y0).
Классический метод Рунге-Кутты является методом 4-го порядка точности и называется методом Рунге-Кутты 4-го порядка.
Формулы
Правило Рунге
Для оценки точности расчёта решения y (например, необходимо рассчитать решение y с помощью значения для y при шаге h/2) на практике можно применять правило Рунге:
yh – значение решения y при шаге h,
yh/2 – значение решения y при шаге h/2,
m – порядок точности формулы.
Условие применения правила Рунге строго задаётся следующим неравенством:
yh – значение решения y при шаге h,
yh/2 – значение решения y при шаге h/2,
y2h – значение решения y при шаге 2h),
m – порядок точности формулы.
Правило Коллатца
При выборе шага h для достижения заданной точности решения дифференциального уравнения вида y’=f(x,y) классическим методом Рунге-Кутты на практике можно применять более простое правило Коллатца:
Формула Ричардсона
Более точным (по крайней мере на порядок выше, т.е. с порядком точности m+1) значением y (по сравнению со значением yh/2) является значение y*, вычисленное или экстраполированное по формуле Ричардсона:
yh – значение решения y при шаге h,
yh/2 – значение решения y при шаге h/2,
m – порядок точности формулы.
- Заметим, что обобщением классического метода Рунге-Кутты является обобщённый метод Рунге-Кутты, используемый для решения систем дифференциальных уравнений.
Другие методы:
- Для решения систем дифференциальных уравнений используется обобщённый метод Рунге-Кутты.
Ссылки
- Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970.
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Участник:Logic-samara