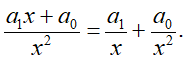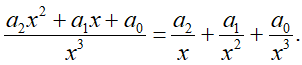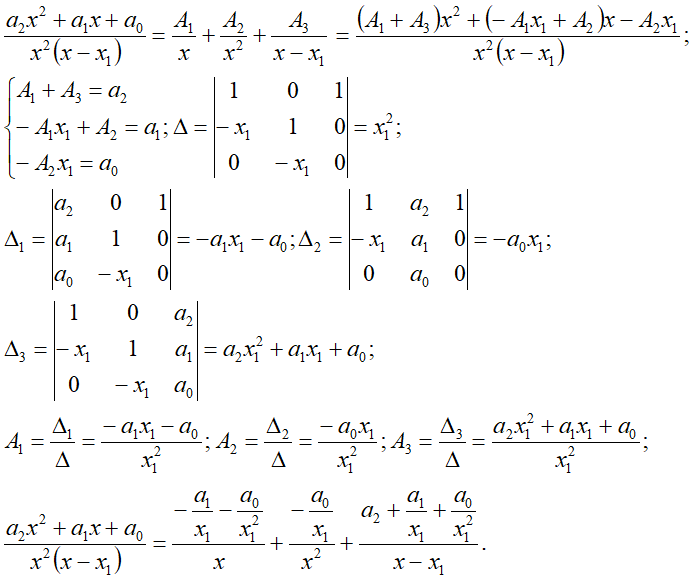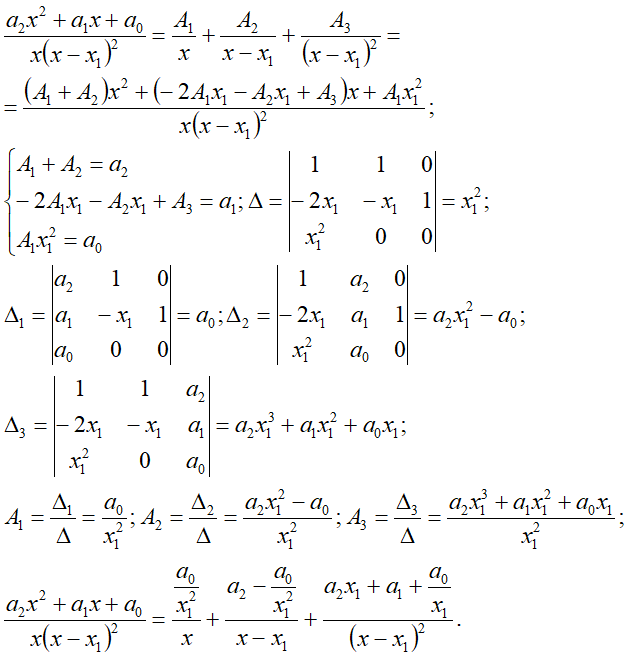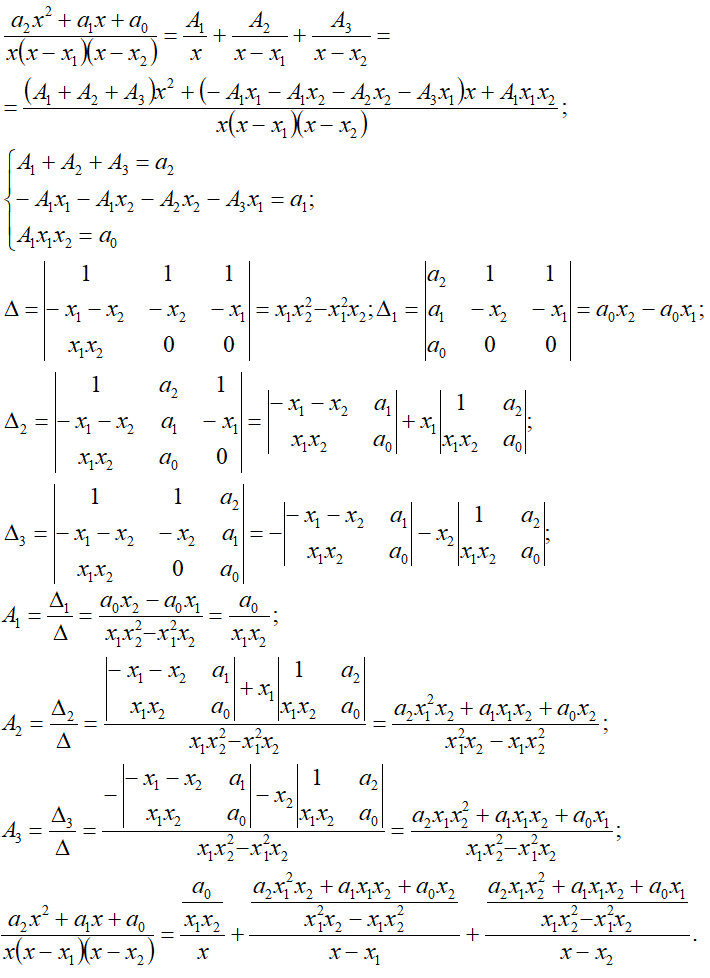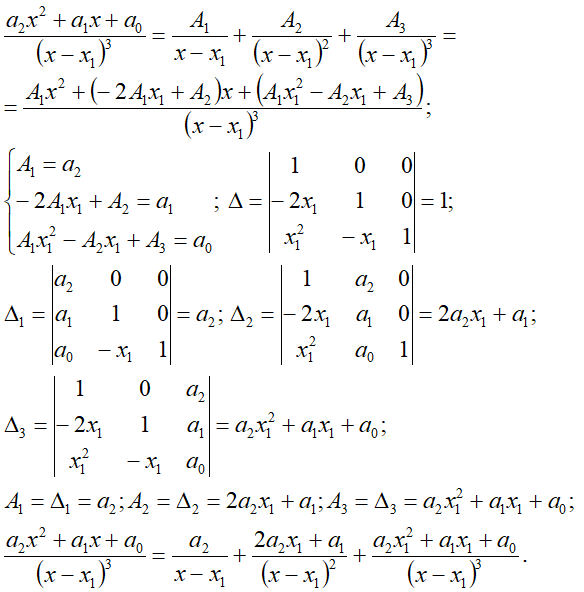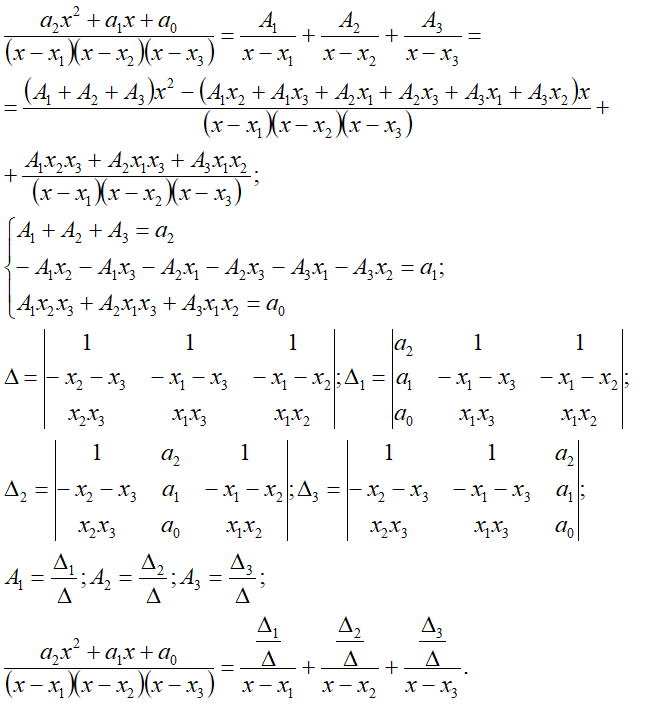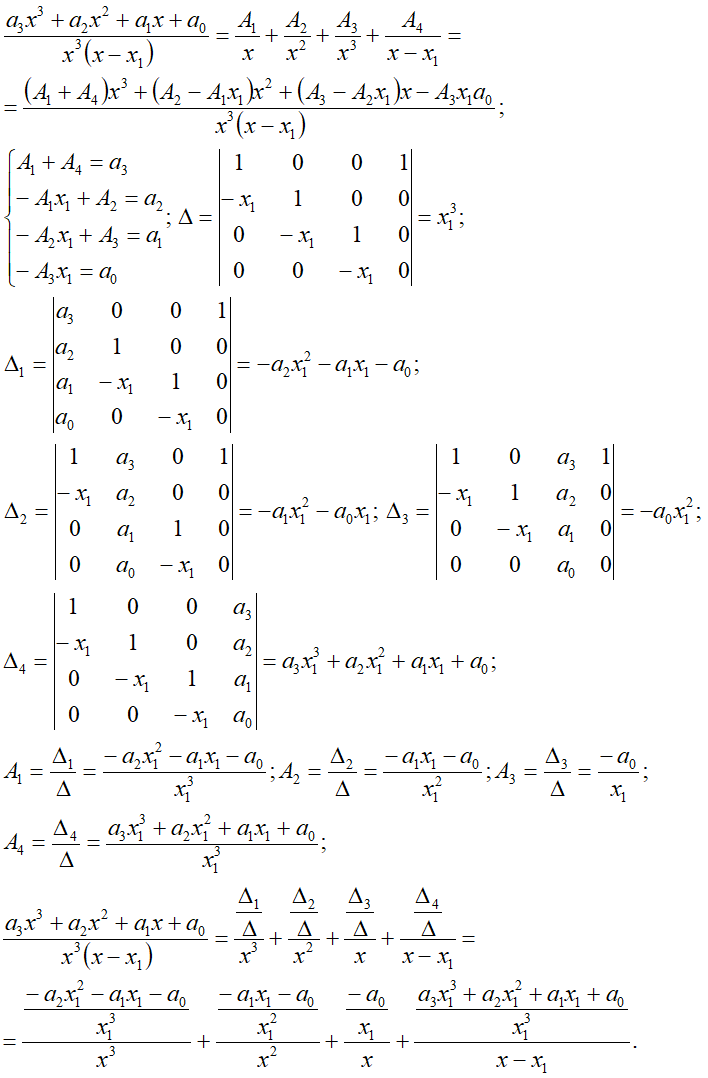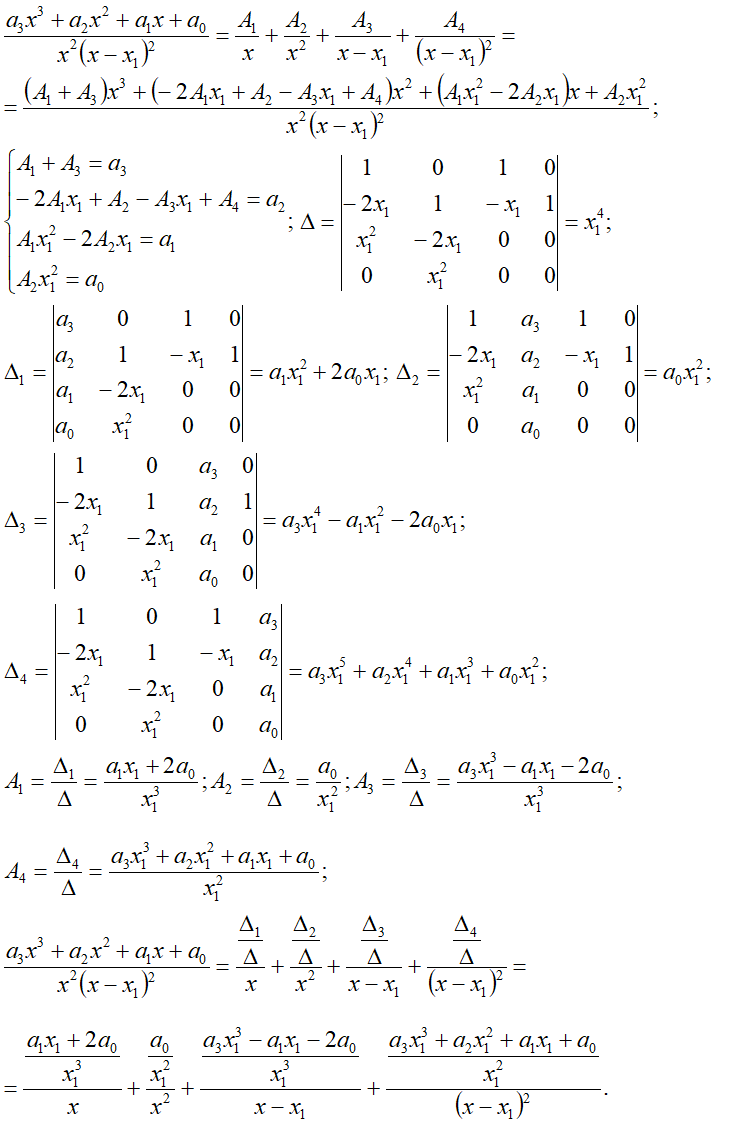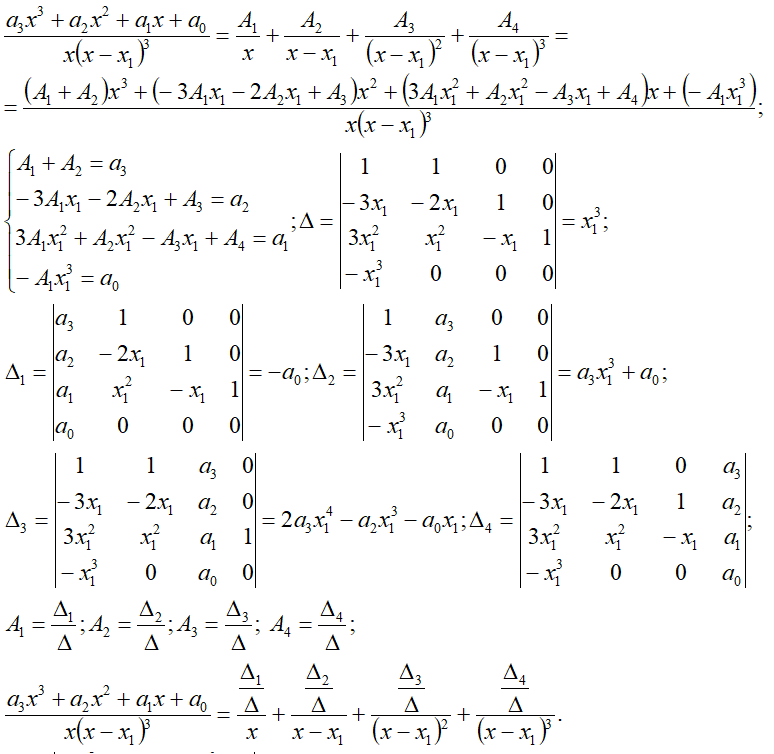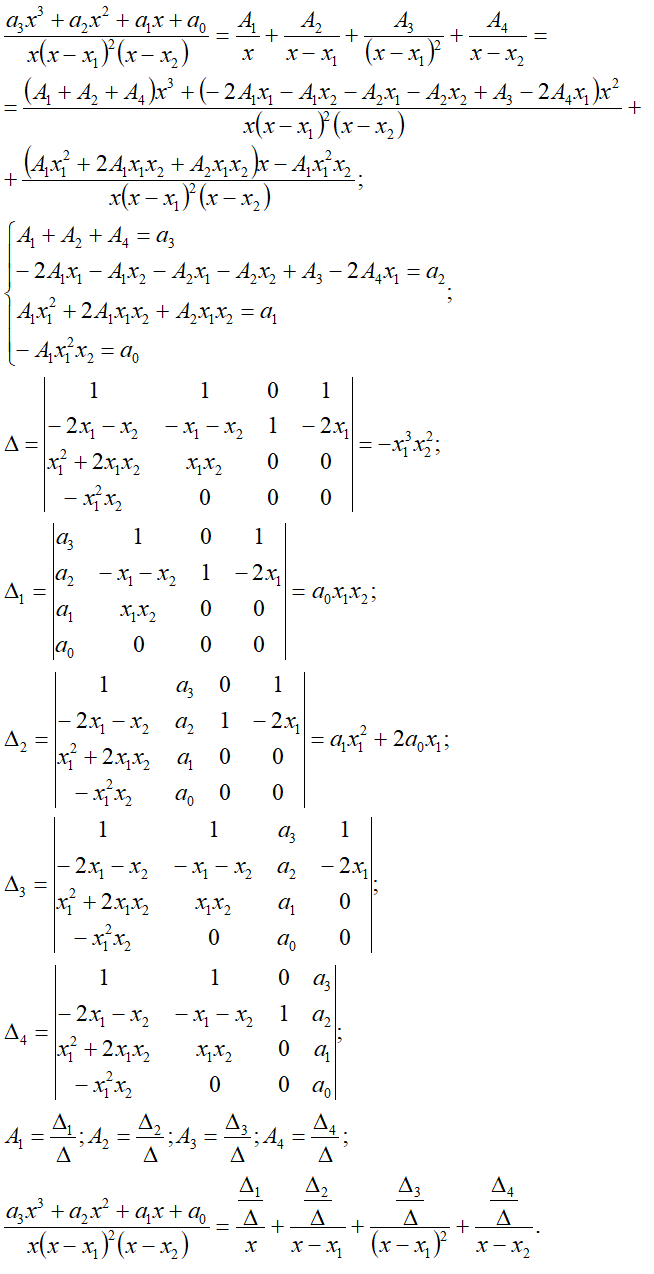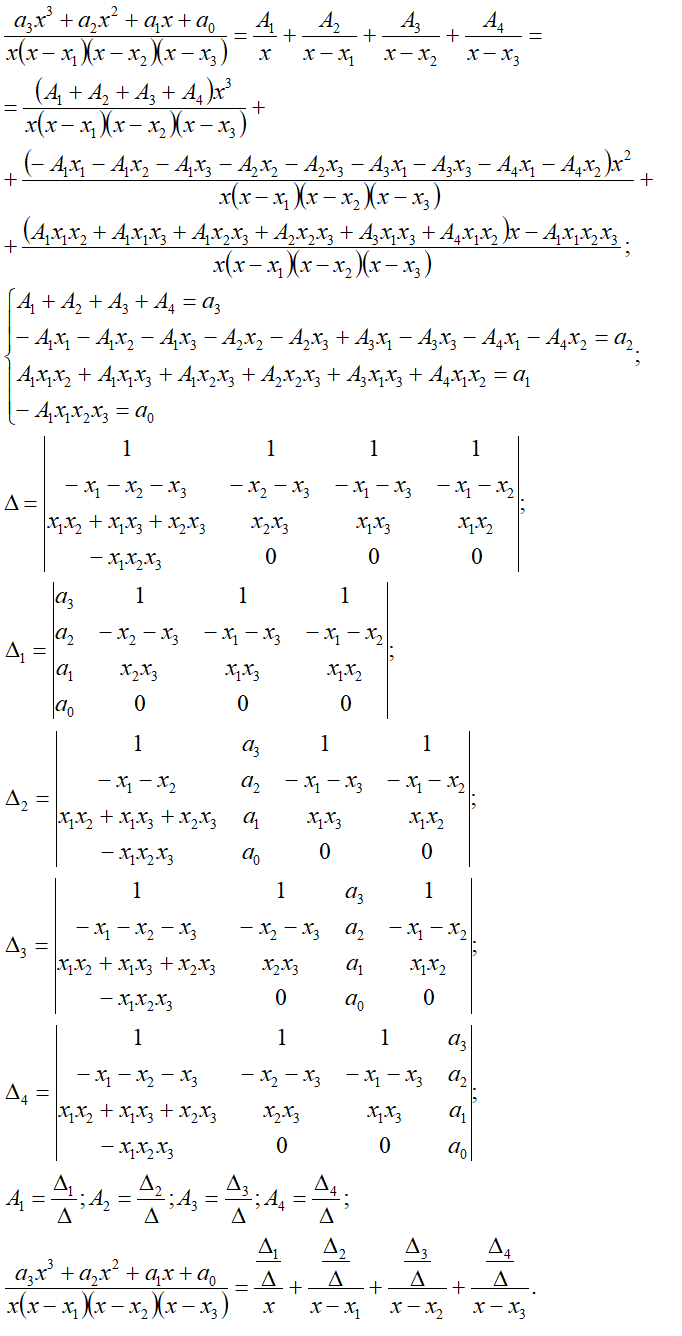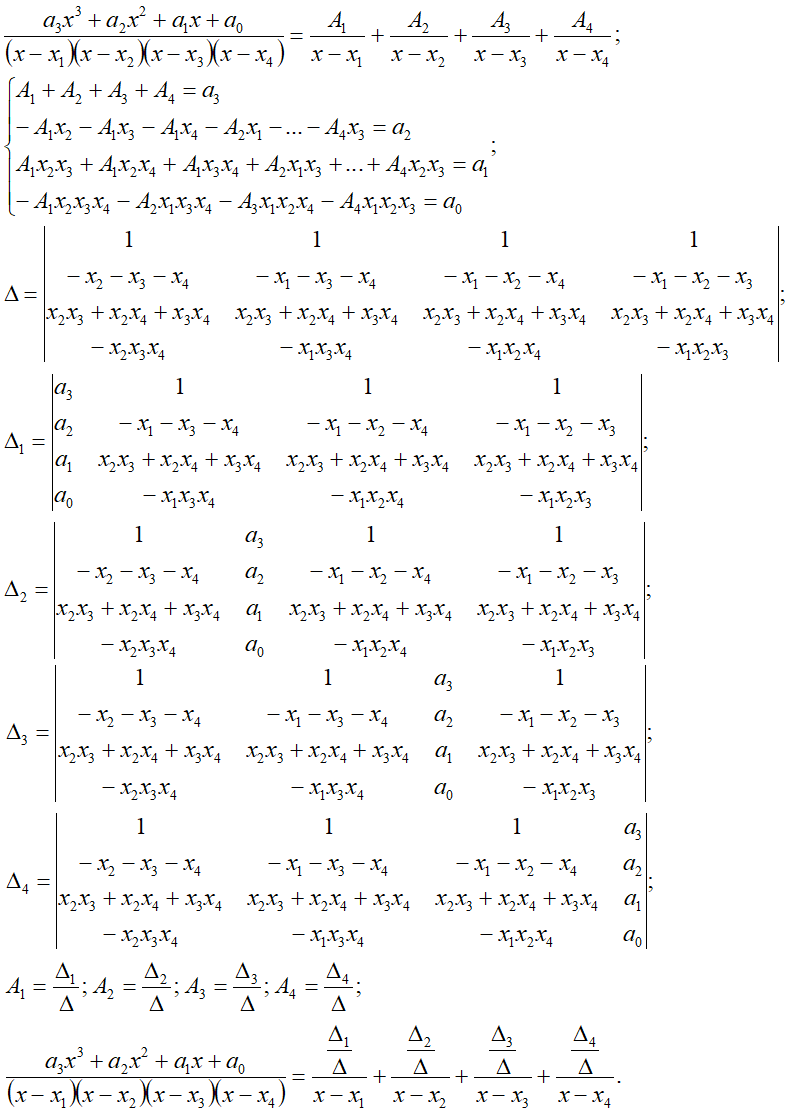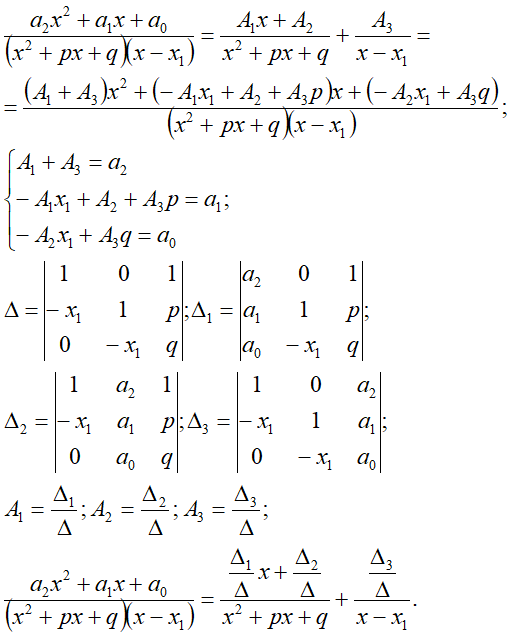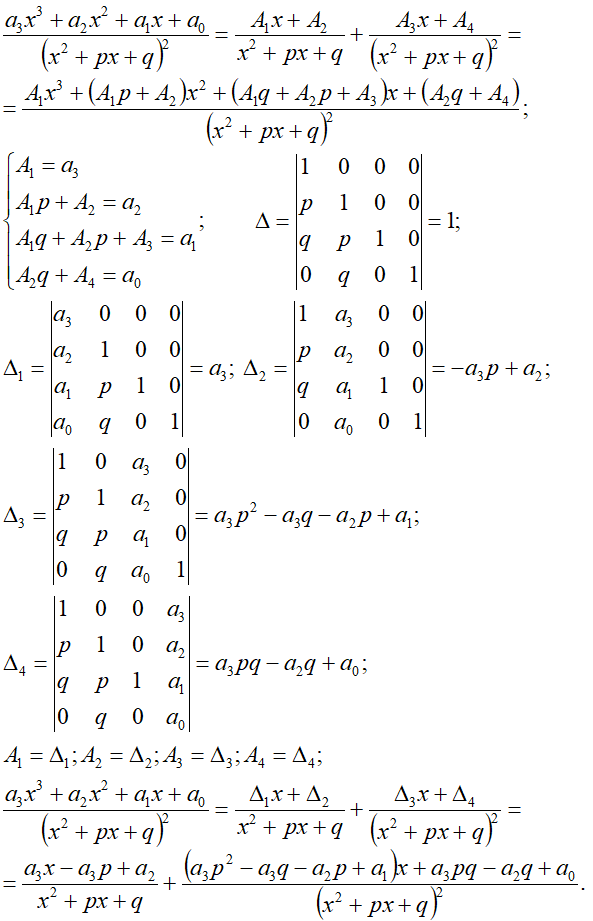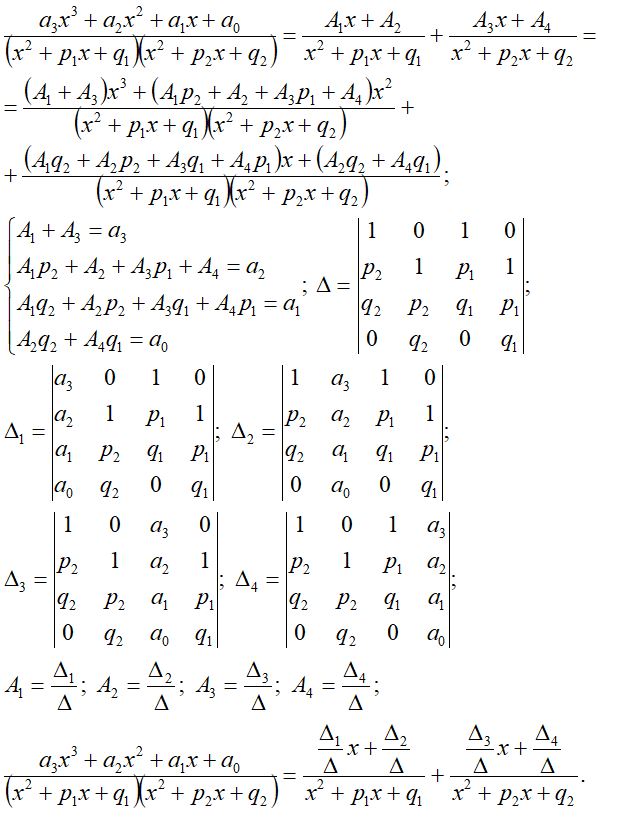Разложение правильной рациональной дроби

Разложение правильной рациональной дроби − это представление в виде простейших рациональных дробей или в виде дробей удобных для интегрирования.

Обозначения

Введём обозначения:

f(x) — дробно-рациональная функция;

f_прав(x) — правильная рациональная дробь;

P_n-1(x) — многочлен степени n-1;

Q_n(x) — многочлен степени n;

x²+px+q — квадратный трёхчлен;

x-x_j — двучлен;

n — степень знаменателя;

n0 — степень x;

n1 — степень x-x₁;

n2 — степень x-x₂;

n3 — степень x-x₃;

n4 — степень x-x₄;

m1 — степень 1-го квадратного трёхчлена;

m2 — степень 2-го квадратного трёхчлена;

a_j, p_j, q_j, p, q — коэффициенты.

Разложение на дроби с двучленами в знаменателе:

n=2

n0=2*

n0=1, n1=1*

n1=2*

n1=1, n2=1*

n=3

n0=3*

n0=2, n1=1*

n0=1, n1=2*

n0=1, n1=1, n2=1*

n1=3*

n1=2, n2=1*

n1=1, n2=1, n3=1*

n=4

n0=4*

n0=3, n1=1*

n0=2, n1=2*

n0=2, n1=1, n2=1*

n0=1, n1=3*

n0=1, n1=2, n2=1*

n0=1, n1=1, n2=1, n3=1*

n1=4*

n1=3, n2=1*

n1=2, n2=2*

n1=2, n2=1, n3=1*

n1=1, n2=1, n3=1, n4=1*

Разложение на дроби с трёхчленами в знаменателе:

n=2

m1=1*

n=3

m1=1, n0=1

m1=1, n1=1

n=4

m1=2

m1=1, m2=1

m1=1, n0=2

m1=1, n0=1, n1=1

m1=1, n1=2

m1=1, n1=1, n2=1

Примечание

• * − разложение удобное для интегрирования

Ссылки

• Участник:Logic-samara