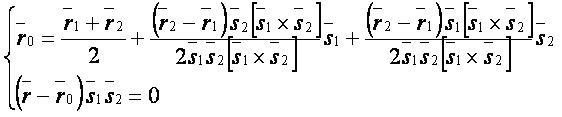Плоскость, равноудалённая от двух прямых
Плоскость, равноудалённая от двух прямых — плоскость, параллельная этим прямым и проходящая через середину перпендикуляра к этим прямым.
Содержание
Обозначения
<math>\bar r=(x,y,z)</math> — радиус-вектор точки плоскости;
<math>\bar r_0=(x_0,y_0,z_0)</math> — радиус-вектор середины перпендикуляра;
<math>\bar r_1=(x_1,y_1,z_1)</math> — радиус-вектор точки первой прямой;
<math>\bar r_2=(x_2,y_2,z_2)</math> — радиус-вектор точки второй прямой;
<math>\bar s_1=(l_1,m_1,n_1)</math> — направляющий вектор первой прямой;
<math>\bar s_2=(l_2,m_2,n_2)</math> — направляющий вектор второй прямой.
Формулы:
Векторная форма:
Координатная форма:
Формулы верны только для скрещивающихся прямых.
Другие уравнения:
- уравнение плоскости, проходящей через три точки;
- уравнение плоскости, равноудалённой от двух точек;
- уравнение плоскости, равноудалённой от двух прямых;
- уравнение плоскости, проходящей через две точки параллельно прямой;
- уравнение плоскости, проходящей через две точки перпендикулярно плоскости;
- уравнение плоскости, проходящей через точку и прямую;
- уравнение плоскости, проходящей через точку перпендикулярно прямой;
- уравнение плоскости, проходящей через точку параллельно плоскости;
- уравнение плоскости, проходящей через точку параллельно двум прямым;
- уравнение плоскости, проходящей через точку перпендикулярно двум плоскостям;
- уравнение плоскости, проходящей через прямую параллельно прямой;
- уравнение плоскости, проходящей через прямую перпендикулярно плоскости.