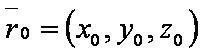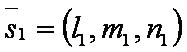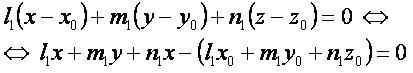Уравнение плоскости, проходящей через точку перпендикулярно прямой
Уравнение плоскости, проходящей через точку перпендикулярно прямой, задаётся равенством нулю скалярного произведения вектора-разности радиусов-векторов точек и направляющего вектора прямой.
Содержание
Обозначения
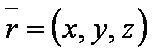
Формулы:
Координатная форма:
Другие уравнения:
- уравнение плоскости, проходящей через три точки;
- уравнение плоскости, равноудалённой от двух точек;
- уравнение плоскости, равноудалённой от двух прямых;
- уравнение плоскости, проходящей через две точки параллельно прямой;
- уравнение плоскости, проходящей через две точки перпендикулярно плоскости;
- уравнение плоскости, проходящей через точку и прямую;
- уравнение плоскости, проходящей через точку перпендикулярно прямой;
- уравнение плоскости, проходящей через точку параллельно плоскости;
- уравнение плоскости, проходящей через точку параллельно двум прямым;
- уравнение плоскости, проходящей через точку перпендикулярно двум плоскостям;
- уравнение плоскости, проходящей через прямую параллельно прямой;
- уравнение плоскости, проходящей через прямую перпендикулярно плоскости.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Выгодский М.Я. Справочник по высшей математике. М.: Наука, 1964, стр.185.