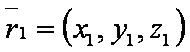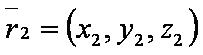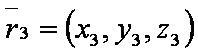Разность векторов — различия между версиями
м |
м |
||
| Строка 1: | Строка 1: | ||
'''Разность векторов''' – это [[вектор]] с координатами, равными разности координат первого и второго векторов, и направлением, совпадающим с направлением отрезка, исходящим из конца второго вектора и направленным в конец первого вектора. | '''Разность векторов''' – это [[вектор]] с координатами, равными разности координат первого и второго векторов, и направлением, совпадающим с направлением отрезка, исходящим из конца второго вектора и направленным в конец первого вектора. | ||
== Обозначения == | == Обозначения == | ||
| − | [[файл:ВЕК71.JPG]] — | + | [[файл:ВЕК71.JPG]] — вектор-уменьшаемое; |
| − | [[файл:ВЕК72.JPG]] — | + | [[файл:ВЕК72.JPG]] — вектор-вычитаемое. |
| + | |||
| + | [[файл:ВЕК73.JPG]] — вектор-разности. | ||
== Формула == | == Формула == | ||
[[файл:Век12.png]] | [[файл:Век12.png]] | ||
Версия 15:04, 23 октября 2024
Разность векторов – это вектор с координатами, равными разности координат первого и второго векторов, и направлением, совпадающим с направлением отрезка, исходящим из конца второго вектора и направленным в конец первого вектора.
Содержание
Обозначения
Формула
Рисунок
Другие операции:
- нахождение длины вектора;
- умножение вектора на число;
- возведение в квадрат координат вектора;
- извлечение корня из координат вектора;
- сложение векторов;
- вычитание векторов;
- умножение координат векторов;
- деление координат векторов;
- скалярное произведение;
- векторное произведение;
- смешанное произведение;
- двойное векторное произведение;
- нахождение угла между векторами;
- ортогонализация векторов.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.