Объём круговой бочки — различия между версиями
м |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 2: | Строка 2: | ||
'''Объём круговой бочки''' — это объём [[Площадь поверхности круговой бочки|бочки]], ограниченной равными основаниями и образованной вращением вокруг вертикальной оси дуги окружности с центром на горизонтальной оси вне вертикальной оси. | '''Объём круговой бочки''' — это объём [[Площадь поверхности круговой бочки|бочки]], ограниченной равными основаниями и образованной вращением вокруг вертикальной оси дуги окружности с центром на горизонтальной оси вне вертикальной оси. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''R''' — радиус образующей дуги окружности; | '''R''' — радиус образующей дуги окружности; | ||
| Строка 24: | Строка 22: | ||
[[файл:ОБО12.JPG]] | [[файл:ОБО12.JPG]] | ||
*Для вывода используется формула 1 '''"[[объём фигуры вращения]]"'''. | *Для вывода используется формула 1 '''"[[объём фигуры вращения]]"'''. | ||
| − | == [[ | + | == [[Объём трёхмерной фигуры|Другие фигуры:]] == |
{{Список ОФВ}} | {{Список ОФВ}} | ||
== Ссылки == | == Ссылки == | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 15:27, 18 февраля 2025
Объём круговой бочки — это объём бочки, ограниченной равными основаниями и образованной вращением вокруг вертикальной оси дуги окружности с центром на горизонтальной оси вне вертикальной оси.
Обозначения
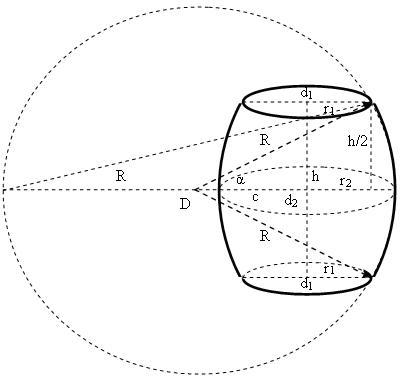
R — радиус образующей дуги окружности;
с — расстояние от центра образующей дуги окружности до вертикальной оси бочки;
h — высота бочки;
α — угол между горизонтальной осью бочки и радиусом образующей дуги окружности, соединяющим центр с вeрхним краем бочки;
r1 — радиус оснований бочки;
r2 — радиус срединной окружности бочки;
Vкруг.боч — объём круговой бочки.
Формула
- Заметим, что когда расстояние от центра образующей дуги окружности до вертикальной оси бочки стремится к нулю, тогда формула объёма круговой бочки превращается в формулу объёма шаровой бочки.
- Заметим, что когда радиус основания бочки стремится к нулю, тогда формула объёма круговой бочки превращается в формулу объёма кокона.
Вывод формулы
- Для вывода используется формула 1 "объём фигуры вращения".
Другие фигуры:
- фигура вращения;
- шар;
- цилиндр;
- конус;
- усечённый цилиндр;
- усечённый конус;
- шаровой сегмент;
- шаровой сектор;
- шаровой слой;
- шаровой клин;
- центральный шаровой клин;
- торовый клин;
- цилиндрическая труба;
- цилиндрическое копыто;
- конусное копыто;
- шаровое копыто;
- параболоидное копыто;
- шаровая бочка;
- круговая бочка;
- параболическая бочка;
- сегментное кольцо;
- тор;
- кокон;
- купол;
- сфероид;
- параболоид.