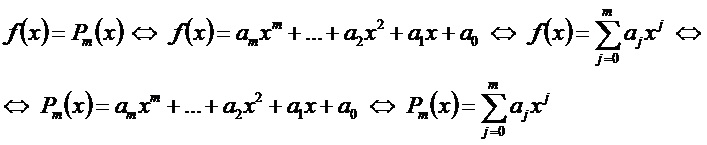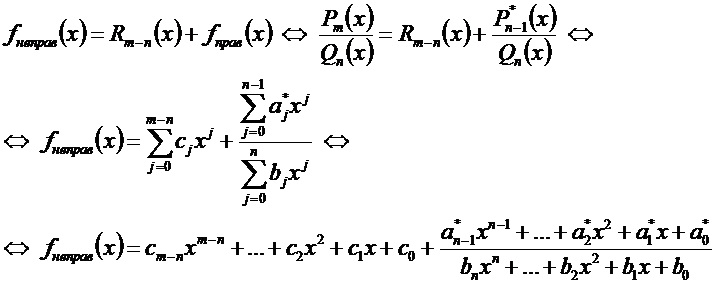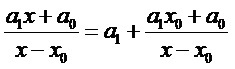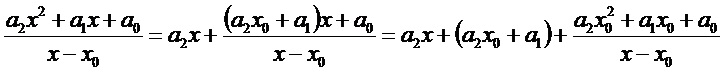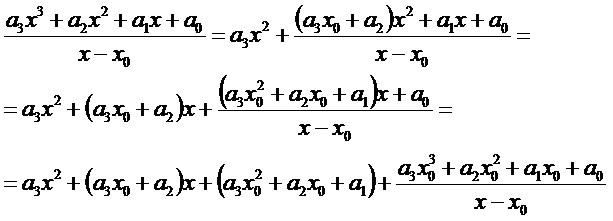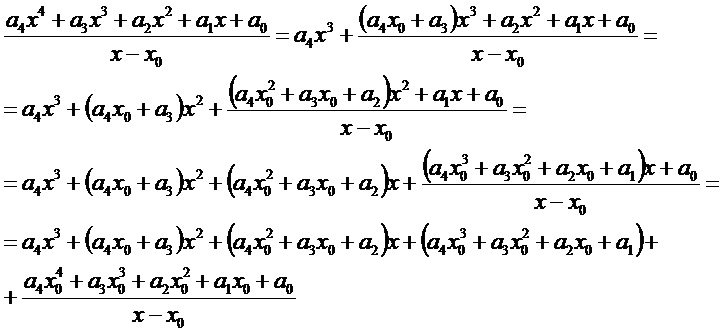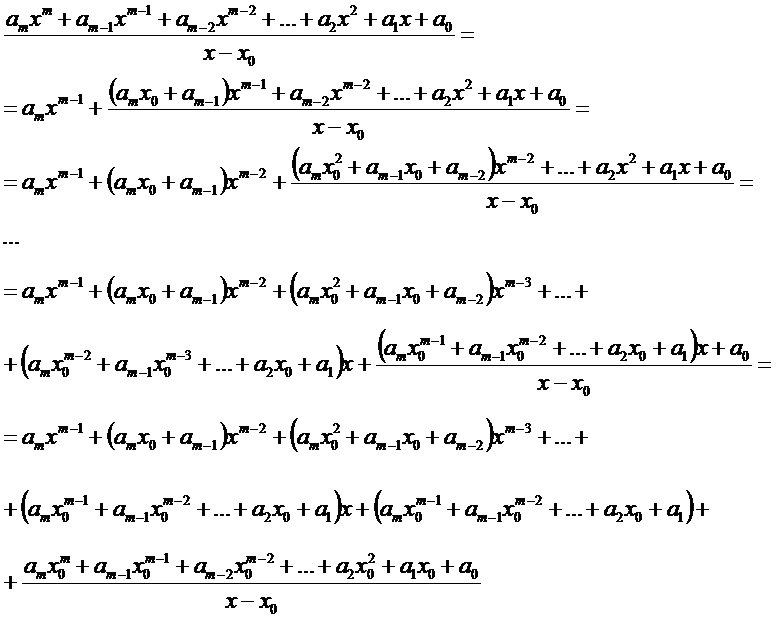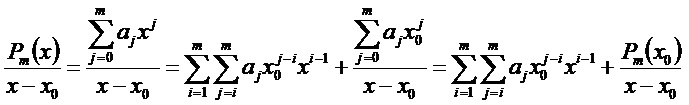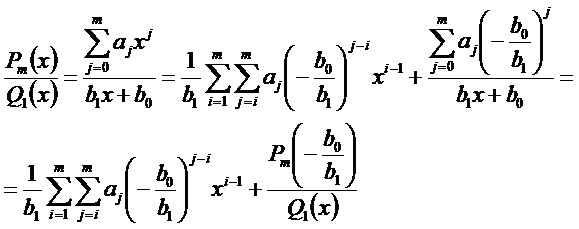Многочлен — различия между версиями
м |
м |
||
| Строка 20: | Строка 20: | ||
== Свойства функции == | == Свойства функции == | ||
[[файл:ДФ02.JPG]] | [[файл:ДФ02.JPG]] | ||
| − | == Деление | + | == Деление многочлена на двучлен '''x-x<sub>0</sub>''' == |
=== '''m=1''' === | === '''m=1''' === | ||
[[файл:ДФ21.JPG]] | [[файл:ДФ21.JPG]] | ||
| Строка 35: | Строка 35: | ||
[[файл:ДФ26.JPG]] | [[файл:ДФ26.JPG]] | ||
| + | == Деление многочлена на двучлен '''x+x<sub>0</sub>''' == | ||
[[файл:ДФ27.JPG]] | [[файл:ДФ27.JPG]] | ||
| + | == Деление многочлена на двучлен '''b<sub>1</sub>x+b<sub>0</sub>''' == | ||
[[файл:ДФ28.JPG]] | [[файл:ДФ28.JPG]] | ||
== [[Функции|Другие функции:]] == | == [[Функции|Другие функции:]] == | ||
Версия 13:57, 9 января 2021
Многочлен − это функция, равная сумме степенных функций с натуральными показателями степени и произвольными коэффициентами.
Содержание
Многочлены
Обозначения
Введём обозначения:
Pm(x) — многочлен степени m;
Pn-1(x) — многочлен степени n-1;
Qn(x) — многочлен степени n;
Rm-n(x) — многочлен степени m-n при m≥n;
aj, bj, cj, x0 — коэффициенты.
Вид функции
Определения
Многочлен называется двучленом, если степень равна 1 и коэффициенты не равны 0, т.е. m=1. Многочлен называется трёхчленом, если степень равна 2 и коэффициенты не равны 0, т.е. m=2.
Свойства функции
Деление многочлена на двучлен x-x0
m=1
m=2
m=3
m=4
m>4
Запишем формулу деления в кратком виде: